第八回 フーリエ逆変換とジョルダンの補題
目的
フーリエ逆変換を行う際、複素積分の積分路をどのように取るべきかを学ぶ。
解答
26. (1)
フーリエ変換の定義より、
\[ \begin{aligned} \hat{f}(k) &= \int_{-\infty}^{\infty} f(x) \mathrm{e}^{-ikx} \mathrm{d} x \\ &= \int_{-a}^{a} \mathrm{e}^{-ikx} \mathrm{d} x \\ &= \left[ \frac{\mathrm{e}^{-ikx}}{-ik} \right]_{-a}^a\\ &= \frac{1}{ik} \left( \mathrm{e}^{ika} - \mathrm{e}^{-ika} \right) \end{aligned} \]
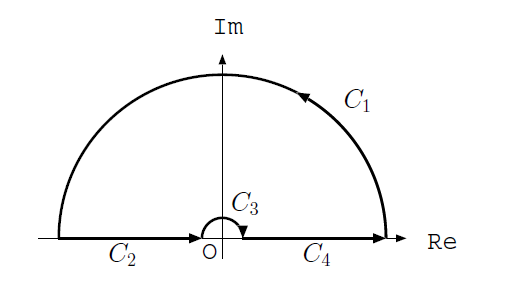
jordan2.png
複素積分を行うための積分路。 全体の積分路\(C = C_1+C_2+C_3+C_4\)は、積分路に特異点が無いから\(0\)。\((x+a)>0\)であれば、十分大きな半径のとき\(C_1=0\)となる。また、\(C_3\)は、半径\(0\)の極限で$-i $であり、求めたい積分は
\[ \int_{-\infty}^{\infty} = \int_{C_2}+\int_{C_4} = -\int_{C_3} \]
から求まる。\((x+a)<0\)の場合は下半面を回らなくてはいけない。
26. (2)
逆フーリエ変換の定義から、
\[ \begin{aligned} f(x) &= \frac{1}{2\pi} \int_{-\infty}^{\infty} \hat{f}(k) \mathrm{e}^{ikx} \mathrm{d} k \\ &= \frac{1}{2\pi i}\int_{-\infty}^{\infty} \left( \frac{\mathrm{e}^{i(x+a)k}}{k} - \frac{\mathrm{e}^{i(x-a)k}}{k} \right) \mathrm{d} k \end{aligned} \]
まず、第一項の積分を計算する。\(x+a>0\)の場合、 積分路\(C\)を図 \(C = C_1 + C_2 + C_3 + C_4\)のように取る。 \(C\)の中には極が無いから、
\[ \int_{C} \frac{\mathrm{e}^{i(x+a)z}}{z} \mathrm{d} z = 0 \]
ジョルダンの補題より大きな半径を取れば\(C_1= 0\)である。 また、積分路\(C_3\)は、一位の極を時計回りに半分だけ回っているから
\[ \int_{C_3} \frac{\mathrm{e}^{i(x+a)z}}{z} \mathrm{d} z = - \pi i \]
である。以上から、
\[ \begin{aligned} \int_{C_1+C_2+C_3+C_4} \frac{\mathrm{e}^{i(x+a)k}}{k} \mathrm{d} k &= &0 \\ \int_{C_2+C_4} \frac{\mathrm{e}^{i(x+a)k}}{k} \mathrm{d} k - \pi i &= &0 \\ \therefore \int_{-\infty}^{\infty} \frac{\mathrm{e}^{i(x+a)k}}{k} \mathrm{d} k &= \pi i \end{aligned} \]
同様に、\(x+a <0\)の時には、
\[ \int_{C_2} \frac{\mathrm{e}^{i(x+a)z}}{z} \mathrm{d} z = - \pi i \]
となる。
まとめると、
\[ \int_{-\infty}^{\infty} \frac{\mathrm{e}^{i(x+a)k}}{k} \mathrm{d} k = \left\{ \begin{array}{cc} \pi i & \quad (x > -a) \\ -\pi i & \quad (x < -a) \end{array} \right. \]
積分の第二項も同様に、
\[ \int_{-\infty}^{\infty} \frac{\mathrm{e}^{i(x-a)k}}{k} \mathrm{d} k = \left\{ \begin{array}{cc} \pi i & \quad (x>a) \\ -\pi i & \quad (x<a) \end{array} \right. \]
以上をまとめると、
\[ f(x) = \left\{ \begin{array}{cc} 0 & \quad x < -a \\ 1 & \quad -a \leq x < a \\ 0 & \quad a \leq x \end{array} \right. \]
となり、確かに元の関数に一致する。
27. (1)
全体をフーリエ変換すると、
\[ (ik)^2 \hat{f} - \hat{f} = {\mathcal F}[\mathrm{e}^{-|x|}] \]
ここで、
\[ \begin{aligned} {\mathcal F}[\mathrm{e}^{-|x|}] &= \int_{-\infty}^{\infty} \mathrm{e}^{-|x|} e^{-ikx} \mathrm{d} x\\ &= \int_{-\infty}^{0} \mathrm{e}^{x} e^{-ikx} \mathrm{d} x + \int_{0}^{\infty} \mathrm{e}^{-x} e^{-ikx} \mathrm{d} x \\ &= \frac{1}{1-ik} + \frac{1}{1+ik}\\ &= \frac{2}{1+k^2} \end{aligned} \]
以上から、
\[ \hat{f}(k) = - \frac{2}{(1+k^2)^2} \]
27. (2)
逆フーリエ変換の定義より、
\[ f(x) = - \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{\mathrm{e}^{ikx}}{(1+k^2)^2} \mathrm{d} k \]
\(x>0\)のとき、複素平面の上を通る半円を積分路とすると、
\[ \int_{-\infty}^{\infty} \frac{\mathrm{e}^{ikx}}{(1+k^2)^2} \mathrm{d} k = \int_C \frac{\mathrm{e}^{ixz}}{(1+z^2)^2} \mathrm{d} z \]
このとき、積分路の中に、2位の極\(z = i\)があるから、 \(F(z) = \displaystyle \frac{2 \mathrm{e}^{ixz}}{(z+i)^2}\)とすれば、
\[ \begin{aligned} \int_C \frac{\mathrm{e}^{ixz}}{(1+z^2)^2} \mathrm{d} z &= \int_C \frac{F(z)}{(z-i)^2} \mathrm{d} z \\ &= 2 \pi i F'(i) \\ &= \frac{2\pi (1+x)}{2} \mathrm{e}^{-x} \end{aligned} \]
すなわち、
\[ f(x) = - \frac{(1+x)}{2} \mathrm{e}^{-x} \]
同様に、\(x<0\)のときは
\[ f(x) = - \frac{(1-x)}{2} \mathrm{e}^{x} \]
まとめると、
\[ f(x) = - \frac{(1+|x|)}{2} \mathrm{e}^{-|x|} \]
27. (3)
\(x>0\)のとき、
\[ \begin{aligned} f(x) &= -\frac{(1+x)}{2}e^{-x}\\ \frac{\mathrm{d}}{\mathrm{d} x} f(x) &= \frac{x}{2}e^{-x}\\ \frac{\mathrm{d}^2}{\mathrm{d} x^2} f(x) &= \frac{(1-x)}{2}e^{-x}\\ \end{aligned} \]
以上から、
\[ \frac{\mathrm{d}^2}{\mathrm{d} x^2} f(x) - f(x) = \mathrm{e}^{-x} \]
\(x<0\)の場合も同様。
解説
関数\(f(x)\)のフーリエ変換\(\hat{f}(k)\)が存在するためには、積分
\[ \int_{-\infty}^{\infty} |f(x)| \mathrm{d} x \]
が有限でなくてはならない。これを 絶対可積分 であるという。 フーリエ変換が可能である条件は、\(f(x)\)が区分的に滑らかで、 絶対可積分であることである。
さて、フーリエ逆変換は、以下の積分で与えられる。
\[ f(x) = \frac{1}{2\pi}\int_{-\infty}^{\infty} \hat{f}(k) \mathrm{e}^{ikx} \mathrm{d} k \]
さて、この積分を、複素積分を用いて
\[ f(x) = \frac{1}{2\pi} \int_{C} F(z) \mathrm{e}^{ixz} \mathrm{d} z \]
を用いて計算したい。このとき、積分路\(C\)をどのように決めるべきだろうか。 ただし、\(|z| \rightarrow \infty\)において\(F(z) \rightarrow 0\)であるとする。 複素積分においては、半円形の積分路が良く取られるが、 半円の半径\(R\)を十分大きくしたときに半円の積分の寄与が\(0\)になる必要がある。
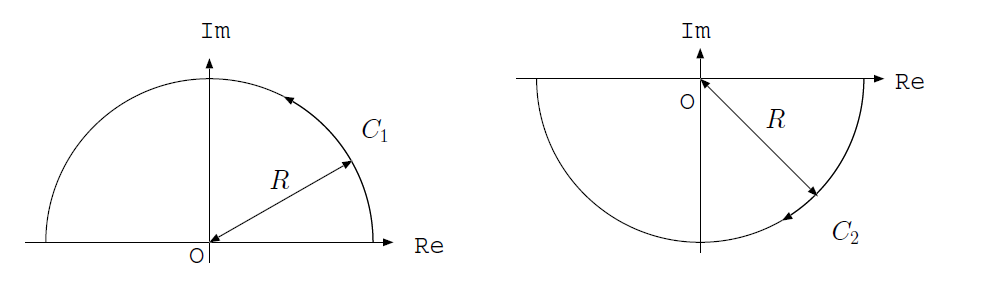
まず、積分路を図の\(C_1\)(複素平面の上半分の半円)のように取ることを考える。 \(u,i\)を実数とし、\(z = u + iv\)としよう。
\[ |\mathrm{e}^{ixz}| = |\mathrm{e}^{ixu - vx}| = \mathrm{e}^{- vx} \]
であるから、\(v \rightarrow \infty\)、すなわち虚軸の上の方で \(\mathrm{e}^{ixz}\)が\(0\)となるためには、\(x>0\)でなくてはならない。 逆に\(x<0\)の時には、\(\displaystyle \lim_{\mathrm{Im} z \rightarrow \infty} \mathrm{e}^{ixz} \rightarrow \infty\)となるため、 積分路を\(C_2\)のように取らなくてはいけない。
以上をまとめて、
\[ \begin{aligned} \lim_{R\rightarrow \infty} \int_{C_1} F(z) \mathrm{e}^{iaz} \mathrm{d} z &= 0 \qquad (a>0)\\ \lim_{R\rightarrow \infty} \int_{C_2} F(z) \mathrm{e}^{iaz} \mathrm{d} z &= 0 \qquad (a<0) \end{aligned} \]
を ジョルダンの補題 という。これはフーリエ逆変換を行う際、 積分路をどのように決めるべきかを考える上で重要である。
jordan.png
ジョルダンの補題。\(F(z)\mathrm{e}^{ikx}\)の積分においては、\(x\)の値によって積分路を変える必要がある。\(x>0\)の場合は\(C_1\)(上半面)を、\(x<0\)の場合は\(C_2\)(下半面)を通る積分路を取る。