NumPyとSciPyの使い方
本講で学ぶこと
- NumPyの使い方
- SciPyの使い方
ライブラリ
スクリプト言語は同時通訳で、コンパイラ言語は事前翻訳である。なんとなく同時通訳で情報を処理するより、事前に全て翻訳しておいた方が実行が早そうな気がするであろう。スクリプト言語よりもコンパイラ言語の方が「同時通訳」というオーバーヘッドがなく、さらにコードの最適化に時間をかけられることもあって、「一般論としては」同じことをするならコンパイラ言語の方が早い。しかし、現実はさほど単純ではない。
一般に、スクリプト言語は豊富な ライブラリ(library) を持つ。ライブラリとは、よく使う機能をパッケージ化したものだ。ライブラリを活用することでよく使う機能を自分で開発する必要がなくなり、楽に早くプログラムを組むことができる。ライブラリは、その言語そのもので書かれたものもあるが、時間がかかる処理についてはCやFortranなどの言語で記述され、事前にコンパイルされている。特に数値計算ライブラリは高度に最適化されていることが多く、よほどのことがなければ自分で直接書くよりPythonからライブラリを呼び出した方が高速に実行できる。本書で扱うNumPyはそのような強力なライブラリの一つだ。
NumPyとSciPy
Pythonには強力なライブラリが多数存在し、それらを使いこなすことで、少ない記述で豊富な機能を素早く実装することができる。今回は、数多くのライブラリの中でも、数値計算、特に行列演算を効率的に行うことができるNumPyと、それを用いて様々な科学的な計算を行うことができるライブラリ、SciPyを使ってみる。
なお、NumPyやSciPyの使い方を覚える必要はない。ただ「PythonにはNumPyやSciPyというライブラリがあり、数行書くだけで行列の固有値問題を解くことができる」ということをぼんやり覚えておいて、将来、必要になった時にそれを思い出して、詳細については本を読むなりウェブで検索するなりすればよい。
NumPyの使い方
NumPyとは
数値計算では、行列を扱うことが非常に多い。行列がからむ演算の中で特に重要なのが、行列同士の積の計算だ。行列と行列の積を行列行列積と呼ぶ。スーパーコンピュータにはTop500という性能ランキングがあり、年に2回ランキングが更新されるが、そこで行われているベンチマークは巨大な連立1次方程式をどれだけ効率的に解くことができるか、という問題である。そして、その計算の中心は行列行列積である。従って、Top500における「スパコンの性能」は、「いかに行列同士の積を早く計算できるか」に依存している。
行列の積の定義そのものは簡単だ。普通にかけば三重ループで計算できる。しかし、現代の計算機では行列の乗算の効率的な実装は非常に面倒であり、「普通」に書くとまったく性能がでない。なにしろ行列行列積は数値計算の根幹をなす演算であり、そこが遅いと非常に広範囲の計算が影響を受けてしまう。そこで、Pythonにおいて行列を効率的に扱うためのライブラリが作られた。それがNumPyである。
NumPy配列の作り方
NumPyを使うには、まずnumpyをインポートする。npという別名をつけるのが慣習である。
import numpy as npNumPy用の配列(NumPy配列)を作成するにはいくつか方法があるが、簡単なのはnp.arrayにリストを与えることだ。
data = np.array([1,2,3])
print(data)[1 2 3]以下は二行二列の行列を作る例である。
a = np.array([[1,2],[3,4]])
print(a)[[1 2]
[3 4]]要素が全てゼロの配列を作るには、zerosを使えばよい。
np.zeros((2,2))z = np.zeros((2,2))
print(z)[[0. 0.]
[0. 0.]]NumPy配列のデータには「型」がある。Pythonのリストは複数の型の混在が許されたが、NumPy配列は全て同じ型でなければならない。NumPy配列のデータの型はdtypeで調べることができる。
print(a.dtype) # => int64
print(z.dtype) # => float64np.arrayで作った場合は、与えたリストから推定された型が使われるが、np.zerosの場合はデフォルトでfloat64の型になる。明示的に型を指定すれば、その型のゼロ要素行列を得ることができる。
z2 = np.zeros((2,2),dtype=np.int64)
print(z2.dtype) # => int64NumPy配列同士の演算
NumPy配列は、「形」を保持しており、shapeでその形を知ることができる。shapeは、タプルの形で返ってくる。
data.shape # => (2,2)形が同じ行列同士は四則演算ができる。ここで*を計算すると、行列積ではなく、「要素ごとの積」を計算することに注意。
b = np.array([[5,6],[7,8]])
print(a*b)[[ 5 12]
[21 32]]行列行列積を計算したい時にはdotを用いる。
c = a.dot(b)
print(c)[[19 22]
[43 50]]NumPy配列の中身
NumPy配列は、どのような「形」でも作ることができる。通常の行列は「行」と「列」のある2次元のデータだが、3次元でも4次元でも作ることができる。しかし、NumPy配列は、実はどのような形であろうとも1次元配列として保存されている。NumPy配列は、1次元のデータshapeプロパティによってどのような形として解釈するかを決めている。reshapeを使うことで、データを変更せずに「形」を変えることができる。
連番の要素を持つ1次元のNumPy配列を作るには、arangeを使う。
a = np.arange(8)
print(a)array([0, 1, 2, 3, 4, 5, 6, 7])このデータを「4行2列の行列」として解釈したNumPy配列を得るには、以下のようにすれば良い。
b = a.reshape((4,2))
print(b)[[0 1]
[2 3]
[4 5]
[6 7]]reshapeにはタプルを渡す。総データ数さえ等しければどのような形にもできる。例えば(2,2,2)という形にもできる。
c = a.reshape((2,2,2))
print(c)[[[0 1]
[2 3]]
[[4 5]
[6 7]]]reshapeは、データ数が合わないとエラーとなる。
a.reshape((4,4)) # => ValueError: cannot reshape array of size 8 into shape (4,4)SciPy
SciPyは、NumPyを基礎にした科学計算ライブラリだ。非常に多くのことができるが、それゆえにその全てを説明することはできない。ここでは、行列の固有値と固有ベクトルだけ求めてみよう。
固有値や固有ベクトルを求めるにはscipy.linalgをインポートすればよい。多くの場合、一緒にnumpyもインポートするであろう。
from scipy import linalg
import numpy as np固有値、固有ベクトルは、linalg.eigで求めることができる。
a = np.array([[1,2],[2,1]])
w, v = linalg.eig(a)これで、wに固有値が、vに固有ベクトルがそれぞれリストの形で返ってくる。
例えば固有値は
print(w) # => [ 3.+0.j -1.+0.j]つまり「3」と「-1」である。一般に固有値は複素数となるが、今回のように入力が実対称行列(もしくはエルミート行列)であることがわかっていれば、エルミート行列向けのeighが使える。
w, v = linalg.eigh(a)
print(w) # => [-1. 3.]エルミート行列の固有値は常に実数であるから、返り値も実数となる。
シュレーディンガー方程式
トンネル効果
原子スケールのようなミクロの世界では、我々が普段目にする世界とは異なり、不思議なことがおきる。そのうちの一つ、「シュレーディンガーの猫」などは聞いたことがあるだろう。今回は量子力学における不思議の一つ、「トンネル効果」をNumPyを使って計算してみよう(課題1)。
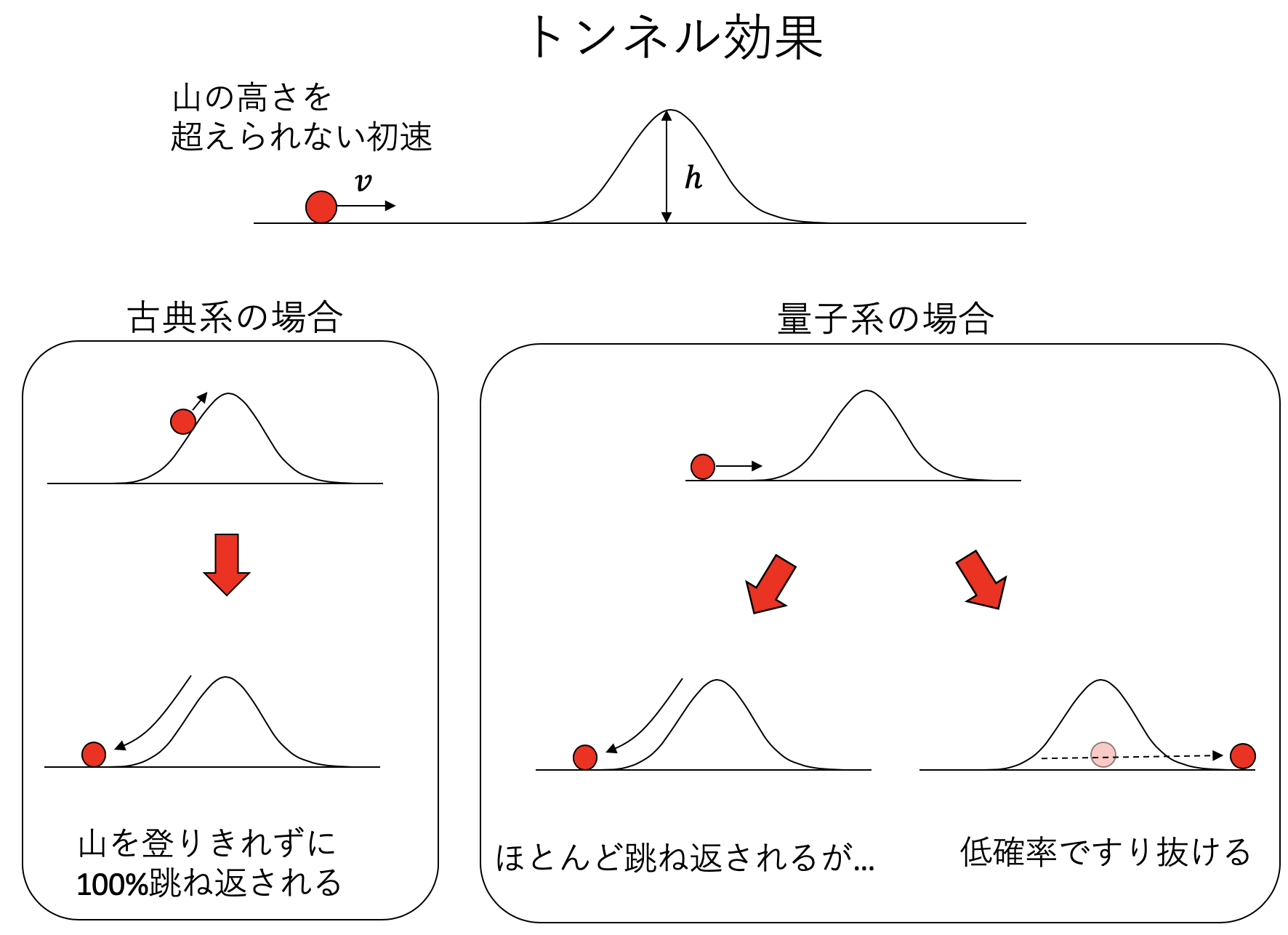
真っ直ぐな道の真ん中に、小さな山があるとしよう。山の高さを\(h\)とする。山の麓にボールを置いて、それに初速を与えて山の方に動かす。初速が、ある程度大きい時には山を超えることができるが、それより小さい場合は山を登りきれずに帰ってくることが予想される。摩擦や回転などを無視して、重力加速度を\(g\)、物体の質量を\(m\)としよう。初速\(v\)を与えると、物体は運動エネルギー\(mv^2/2\)を得る。山の頂上に行くためには、ポテンシャルエネルギー\(mgh\)が必要だ。以上から、山を登り切るためには\(mv^2/2 > mgh\)だけのエネルギーが必要であるため、\(v < \sqrt{2gh}\)の時には山を登り切ることができない。このように、量子力学が必要ないようなマクロな世界を古典系と呼ぶ。古典系では、初速が足りなければなんどトライしても山を超えることはできない。
しかし、物体の波動性が効いてくるようなミクロな領域では古典系とは異なることがおきる。初期エネルギーが山を超えるのに必要なエネルギーより小さい場合でも、低確率で山をすり抜けて向こう側に行ってしまう。まるでトンネルを抜けたかのように見えるので、トンネル効果と呼ばれる。トンネル効果は、例えば走査型トンネル顕微鏡などに応用されている。
シュレーディンガー方程式
さて、マクロな物体の運動はニュートンの運動方程式で記述されるが、ミクロな現象は量子力学に支配されている。例えば電子の位置などはシュレーディンガー方程式に従う。時間非依存・1体・1次元のシュレーディンガー方程式は以下のように書ける。
\[ \left( \frac{-\hbar^2}{2m} \frac{d^2 }{d x^2} + V(x) \right) \psi(x) = E \psi(x) \]
ここで、\(\hbar\)はプランク定数、\(m\)は質量である。\(V(x)\)はポテンシャルで、位置\(x\)による「高さ」を表しており、例えば先程の山の高度だと思えば良い。この方程式を解くことで波動関数\(\psi(x)\)を求めることができる。波動関数は、その二乗が「その位置に粒子(例えば電子)を見出す確率」となる。したがって、シュレーディンガー方程式を解くとは、どの場所にどれくらいの確率で粒子が存在するかの確率を求めることに対応する。以下、簡単のため、\(\hbar^2/2m\)を\(1\)とする単位系をとる。
さて、この方程式を計算機で解くために離散化する。微分方程式の離散化は後の回に説明するので、以下はざっと読み飛ばして良い。先程の式には\(x\)に関する二階微分があったが、これを
\[ \frac{d^2 \psi}{d x^2} \sim \frac{\psi(x+h) - 2 \psi(x) + \psi(x-h) }{h^2} \]
と近似する。離散化により、波動関数\(\psi(x)\)は、ベクトル\(\vec{v}\)で表すことができる。\(h\)を1とし、\(\vec{v}\)のi番目の成分を\(v_i\)とすると、上記の微分は
\[ \frac{d^2 \psi}{d x^2} \sim v_{i+1} - 2 v_i + v_{i-1} \]
と表現できる。右辺は配列の要素の加減算なのでプログラムするのは簡単だ。これを先程の微分方程式に代入すると、最終的に
\[ -v_{i+1} + 2 v_i - v_{i-1} + V_i v_i = E v_i \]
という式が得られる。ただし、\(V_i\)は\(V(x)\)を離散化してベクトルにした時の\(i\)番目の要素だ。これを行列とベクトルで書き表すと、
\[ H \vec{v} = E \vec{v} \]
という、行列の固有値問題になった。ただし\(H\)は以下のような要素を持つ行列である。

長々と書いたが、この式を理解する必要はない。要するに「ミクロな世界はシュレーディンガー方程式で記述され、シュレーディンガー方程式は離散化により行列の固有値問題になる」ということがわかればよい。行列の固有値問題を解くことで、任意のポテンシャル形状\(V(x)\)で、電子がどのように分布するかを計算することができる。課題では井戸型ポテンシャルに閉じ込められた電子の存在確率を計算することで、トンネル効果を見てみよう。
特異値分解による画像圧縮
線形代数を学んでいれば、異なる行列の積を定義できることを覚えているだろう。例えばm行n列の行列と、n行k列の行列の積をとると、新たにできる行列はm行k列となる。
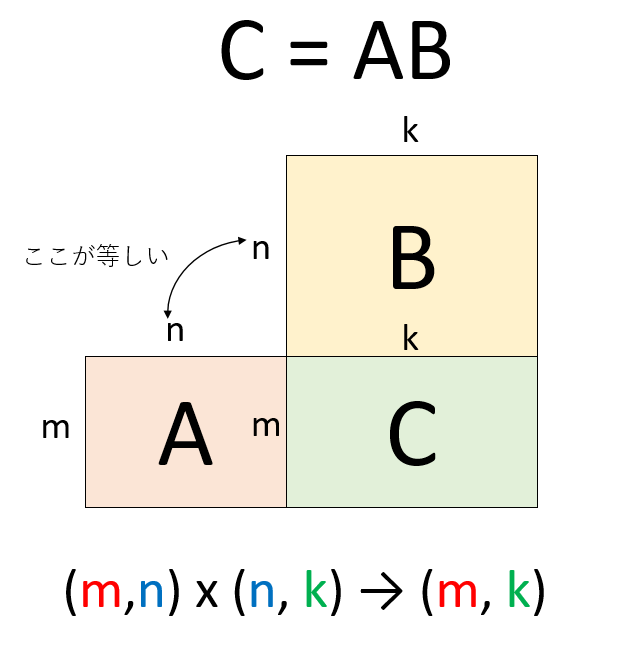
(m,n)の形をした行列と(n,k)の形をした行列から(m,k)の形をした行列ができるのだから、例えば10行2列の行列\(A\)と、2行10列の行列\(B\)の積は、10行10列の行列\(C\)になる。この時、\(A\)、\(B\)の要素数はそれぞれ20個、合計40個だが、積をとってできる行列\(C\)の要素数は100個となり、\(A\)、\(B\)の要素数の合計よりも多い。この事実を利用して、\(C\)という大きな行列を、\(A\)と\(B\)という「細長い」行列の積で近似することを考えよう。
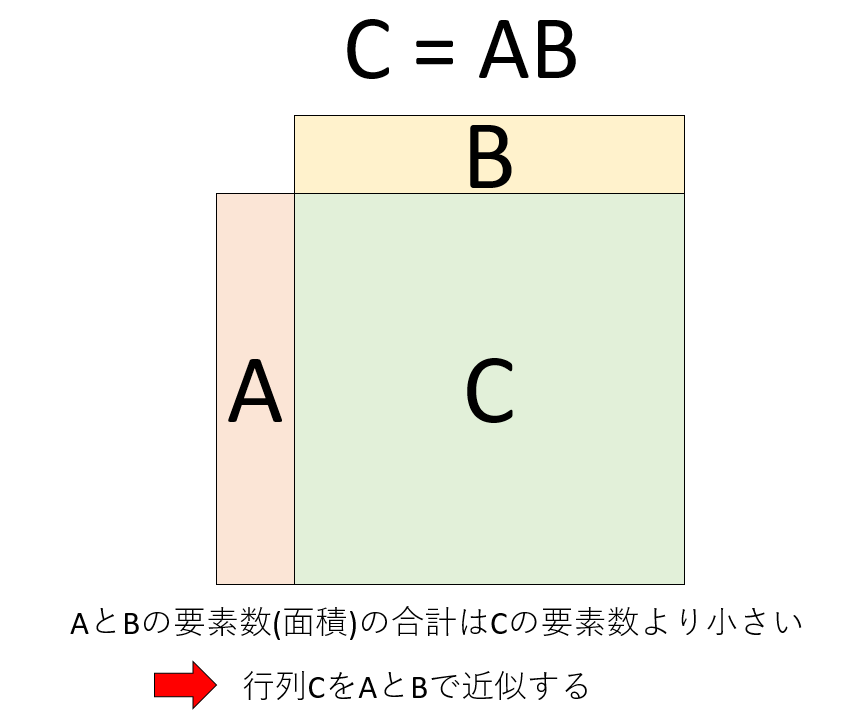
つまり、何か行列\(X\)が与えられた時、\(\tilde{X} = AB\)という行列を作り、\(\tilde{X}\)が元の行列\(X\)をよく近似するように、なるべく「細長い」行列\(A\)、\(B\)を探しなさい、という問題である。このような行列は、特異値分解(Singular Value Deconposition, SVD)という方法で作ることができる。
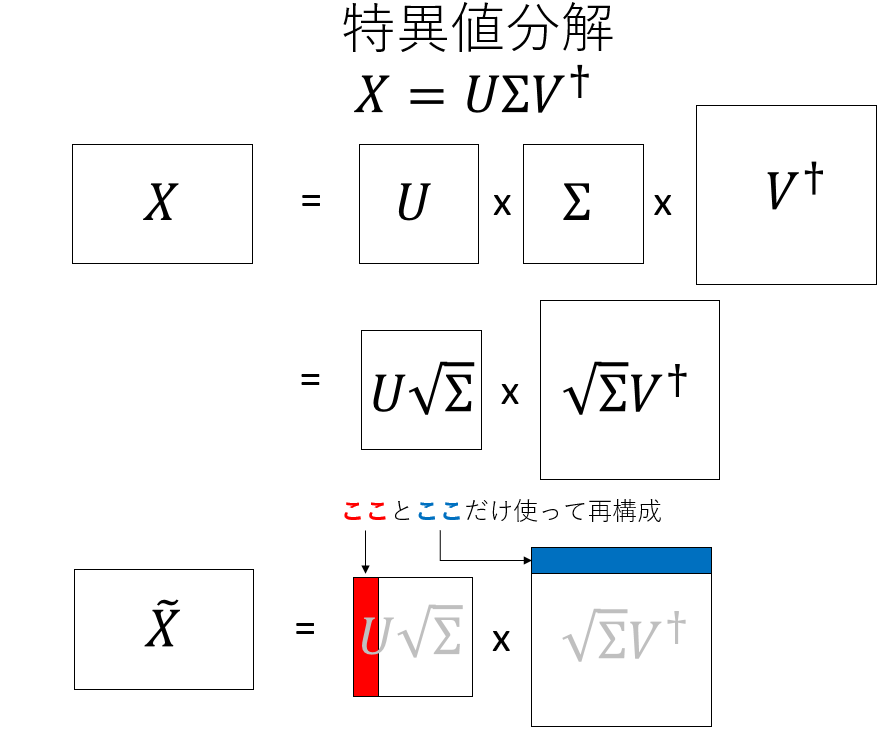
いま、\(X\)というm行n列の行列が与えられた時、以下のように「分解」ができる。
\[ X = U \Sigma V^{\dagger} \]
ただし、\(U\)はm行m列、\(V^{\dagger}\)はn行n列のそれぞれ正方行列であり、\(\Sigma\)は対角行列である。この\(\Sigma\)の対角成分を特異値と呼び、全て非負の実数に取ることができる。
さて、真ん中の\(\Sigma\)を2つの\(\sqrt{\Sigma}\)にわけて、それぞれ左右にくっつけると、\(X = A B\)の形に書くことができる。この\(A\)の行列の「右端の帯」と、\(B\)の行列の「上端の帯」の積をとってできる行列\(\tilde{X}\)は、元の行列\(X\)と同じ形であり、かつ良い近似になっている。これを「行列の低ランク近似」と呼ぶが、ここではその詳細は触れない。
課題では、行列の特異値分解と低ランク近似を利用して、画像圧縮をしてみよう(課題2)。
NumPyとSciPyの使い方:課題
課題1:シュレーディンガー方程式
シュレーディンガー方程式を離散化することで数値的に解いてみよう。新しいノートブックを開き、tunneling.ipynbという名前で保存せよ。
1. ライブラリのインポート
最初のセルはいつもどおりライブラリのインポートである。
import matplotlib.pyplot as plt
from scipy import linalg
import numpy as np2. 行列の作成
次に、ポテンシャル\(V(x)\)に対応するベクトルVと、微分方程式を差分化した行列Hを作成する。
N = 32
V = np.zeros(N)
V[N // 4:3 * N // 4] = -5.0
H = np.zeros((N, N))
for i in range(N):
i1 = (i + 1) % N
i2 = (i - 1 + N) % N
H[i][i] = 2.0 + V[i]
H[i][i1] = -1
H[i][i2] = -13. 固有値と最低固有エネルギー
得られた行列の固有値、固有ベクトルを求め、さらに固有値の中でもっとも値が小さいもののインデックスを求めよう。3つ目のセルに以下を入力、実行せよ。
w, v = linalg.eigh(H)
i0 = np.argmin(w)
print(w[i0])最小値を求めるだけならnp.min(w)で良いが、後で対応する固有ベクトルを使うのにインデックスが必要なので、np.argmin(w)を利用している。
実行してみると、-5よりも若干大きな値が表示されたはずである。これが「閉じ込めエネルギー」と呼ばれるものだ。なぜ「閉じ込め」と呼ばれるかは次のステップで可視化することで明らかとなる。
4. 波動関数の可視化
井戸型ポテンシャルに閉じ込められた波動関数の可視化をしてみよう。波動関数は、その二乗が電子の「存在確率」を表す。先ほど得た「最低固有エネルギー」に対応する固有ベクトルを二乗したものを、ポテンシャルと一緒にプロットしてみよう。4つ目のセルに以下を入力せよ。
v = v[:, i0]
v = v * v
plt.plot(v * 20 + w[i0])
plt.plot(V)波動関数とポテンシャルが同時にプロットされたはずである。波動関数は「そこに電子が存在する確率」である。その存在確率が少しだけ井戸の外にしみだしていることがわかるはずである。これが「トンネル効果」と呼ばれるものだ。
課題2:行列の低ランク近似による画像処理
特異値分解による行列の近似を利用して、画像圧縮をしてみよう。高さhピクセル、幅wピクセルのモノクロ画像は、それぞれのピクセルの値を要素だとおもえば、h行w列の行列と思うことができる。それを特異値分解し、「細長い」二つの行列に分離することでデータを圧縮する。「細長い行列」の行列積をとると元の大きさに戻るので、それを可視化することで復元された画像を得ることができる。
新しいノートブックを開き、svd.ipynbという名前で保存せよ。
1. ライブラリのインポート
1つ目のセルにで、必要なライブラリをインポートしよう。
import urllib.request
import numpy as np
from PIL import Image
from scipy import linalg
from io import BytesIO2. 画像のダウンロード関数
圧縮する元の画像をダウンロードする関数を実装しよう。2つ目のセルで以下を実行せよ。
def download(url):
with urllib.request.urlopen(url) as f:
data = f.read()
return Image.open(BytesIO(data))3. 画像の表示
ダウンロード関数のテストをしよう。3つ目のセルで以下を実行せよ。
URL = "https://kaityo256.github.io/python_zero/numpy/stop.jpg"
download(URL)カラー画像が表示されれば成功である。
4. モノクロへの変換
先ほどダウンロードした画像はカラー画像であり、各ピクセルにR、G、Bの値が紐づけられている。このままでは行列とみなすことができないので、モノクロ化する関数を実装しよう。4つ目のセルに以下を実装せよ。
def mono(url):
img = download(url)
gray_img = img.convert('L')
return gray_img5. モノクロ変換のテスト
モノクロに変換できるか確認しよう。5つ目のセルで以下を実行せよ。
URL = "https://kaityo256.github.io/python_zero/numpy/stop.jpg"
mono(URL)モノクロ画像が表示されれば成功である。
6. 画像の低ランク近似
画像を特異値分解により低ランク近似する関数を実装しよう。6つ目のセルに以下を入力せよ。
def svd(url, ratio):
gray_img = mono(url)
a = np.asarray(gray_img)
w, _ = a.shape
rank = int(w * ratio)
u, s, v = linalg.svd(a)
ur = u[:, :rank]
sr = np.diag(s[:rank])
vr = v[:rank, :]
b = ur @ sr @ vr
return Image.fromarray(np.uint8(b))画像データをasarrayに渡すことでそのままNumPy配列にすることができる。その配列をlinalg.svdに渡せば特異値分解完了である。その後、ratioで指定された特異値の数だけ残して画像を再構成している。
7. 画像の低ランク近似の確認
先程実装した低ランク近似関数を確認しよう。7つ目のセルで以下を実行せよ。
URL = "https://kaityo256.github.io/python_zero/numpy/stop.jpg"
ratio = 0.1
svd(URL, ratio)上記を実行すると、画像のピクセル値を行列要素だと思って、行列を特異値分解により低ランク近似してから再構成した画像が表示される。ratioは、使う情報の割合であり、その数字を増やすとたくさん情報を使うので近似精度が高くなり、減らすと低くなる。ratio = 0.05の場合と、ratio = 0.2の場合も確認し、画像がどうなるか確認せよ。
発展課題
インターネットで適当な画像を探し、上記の手続きで低ランク近似をせよ。適当な画像で右クリックし、「画像アドレスをコピー」等でアドレスを取得できる。そのアドレスをURLに指定せよ。画像フォーマットはJPG形式とし、あまり大きな画像でない方がよい。また、文字を含む画像である方が圧縮の精度がわかりやすい。
URL = # ここを指定せよ
ratio = 0.1
svd(URL, ratio)いくつかのratioの値を試してみて、画像の「近似のしやすさ」「再現性が良いところ、悪いところ」等について気づいたことがあれば記述せよ。また、圧縮画像に「黒い斑点」のようなものが現れる場合があるのはなぜか、考察せよ。
余談:人外
「人外」という言葉がある。「じんがい」と読む。主にファンタジーなどの世界において、獣人や精霊、妖精など、人としての外見を持つが、基本的に人よりも高次の存在を「人外」と呼ぶことが多い。世界観にもよるが、基本的に「人外」は人間より優れた能力を持ち、通常の人間が敵う相手ではない、強大な存在として描かれることが多い。いつの頃からか、この「人外」という言葉が「同じ人間とは思えないような、卓越した成果を挙げている人間」を指すようになった。筆者は「同じ人とは思えないプログラム能力を持つ存在」という意味で使っている。この意味での用例の初出がどこかはわからない。おそらく「競技プログラム」界隈から言われるようになったのではないかと思われる。
本稿の読者は大学生を想定しているが、20年近く生きていれば、「あ、こいつには絶対にかなわない」というような、才能の差を感じて絶望したことが一度や二度はあるであろう。おそらく君たちの二倍以上生きている筆者も、自慢じゃないがこれまでなんども「才能の差」に絶望してきた。特に「プログラミング」は、「できる人」と「できない人」の差が極めて大きく開く分野である。定義にもよるが、「できる人」と「できない人」の生産性はかるく桁で変わってしまう。そして、「この人、本当に人間なんかいな」という「人外プログラマ」の作るものを目の当たりにして驚嘆し、自分と比較して絶望し、その後に達観するのである。
我々一般人は、普通に生きていれば「人外」とぶつかる可能性は低い。むしろぶつからないように生きるのが正しい道である。しかし、何かとちくるって、一般人であるにもかかわらず「世界一になりたい」という野望を抱いてしまうと不幸である。なんでもよいが、何かの処理の最速、世界一を目指すと、極めて高確率で「人外」とぶつかる。人外は、その絶対数が少ない希少種である。しかし、何か数値化され、「世界一」が客観的に定義できる場所には(それがどんなにマイナーな分野であっても)必ず生息している。世界一になるためには、彼らに勝たなければいけない。ファンタジーでの定番、圧倒的な存在である人外をどうやって人間が討伐するか、という問題図式である。
ではどうすればいいのか? まだどの分野でも世界一になったことがない僕は、もちろんその答えを持っていない。