Day 5 :二次元反応拡散方程式
Day 4では一次元拡散方程式を領域分割により並列化した。後はこの応用で相互作用距離が短いモデルはなんでも領域分割できるのだが、二次元、三次元だと、一次元よりちょっと面倒くさい。後、熱伝導方程式は、「最終的になにかに落ち着く」方程式なので、シミュレーションしててあまりおもしろいものではない。そこで、二次元で、差分法で簡単に解けて、かつ結果がそこそこ面白い題材として反応拡散方程式を取り上げる。
反応拡散方程式
反応拡散方程式(reaction-diffusion system)とは、拡散方程式に力学系がくっついたような系で、様々なパターンを作る。例えば「reaction-diffusion system」でイメージ検索してみて欲しい。生物の模様なんかがこの方程式系で説明されたりする。
世の中には様々な反応拡散方程式があるのだが、ここではGray-Scottモデルと呼ばれる、以下の方程式系を考えよう。
\[ \frac{\partial u}{\partial t} = D_u \Delta u + u^2 v - (F+k)u \]
\[ \frac{\partial v}{\partial t} = D_v \Delta v - u^2 v + F(1-v) \]
これは\(U\)と\(V\)という化学物質の化学反応を模した方程式である。 \(U\)が活性化因子、\(V\)が抑制因子と呼ばれる。 \(U\)と\(V\)の濃度を\(u\)、\(v\)とすると、\(V\)の濃いところでは\(U\)が生成されないことがわかる。 \(D_u\)や\(D_v\)は拡散係数であり、\(D_v/D_u = 2\)にとる。つまり、\(V\)の方が拡散しやすい物質となる。 この方程式を計算することにしよう。
ちなみに、世界で広く使われている表記と\(U\)と\(V\)が逆のようである。プログラム全部書き終わってから気がついたので、申し訳ないがそのままにする。
シリアル版
まず、ある点におけるラプラシアンを返す関数laplacianを用意しよう。中央差分で表現すると、上下左右の点との平均との差で表現すれば良いので、こう書ける。
double laplacian(int ix, int iy, vd &s) {
double ts = 0.0;
ts += s[ix - 1 + iy * L];
ts += s[ix + 1 + iy * L];
ts += s[ix + (iy - 1) * L];
ts += s[ix + (iy + 1) * L];
ts -= 4.0 * s[ix + iy * L];
return ts;
}また、\(u\)と\(v\)の力学系の部分を計算する関数も作っておこう。
double calcU(double tu, double tv) {
return tu * tu * tv - (F + k) * tu;
}
double calcV(double tu, double tv) {
return -tu * tu * tv + F * (1.0 - tv);
}さて、差分を計算する際、\(t+1\)ステップ目の計算に\(t\)ステップの物理量を使う。 もしここで\(t\)の値をどんどん更新してしまうと、ある場所の物理量を計算する時に\(t\)の値と\(t+1\)の値が混ざっておかしなことになる。実は、一次元拡散方程式ではそれを防ぐため、一度\(t\)の時の値を別の領域にコピーして、それを使って\(t+1\)の値を計算するようにしていた(要するに手抜きである)。しかし、二次元でこれをやるとさすがにコピーのオーバーヘッドが大きい。
そこで、同じ物理量を表す配列を二本ずつ用意して、奇数時刻と偶数時刻で使い分けることにしよう。
具体的にはuに対してu2という配列も用意しておく。
いま偶数時刻だとするとu2からuを、奇数時刻ならuからu2を計算する。
というわけで、1ステップ時間発展を行う関数calcはこう書ける。
void calc(vd &u, vd &v, vd &u2, vd &v2) {
for (int iy = 1; iy < L - 1; iy++) {
for (int ix = 1; ix < L - 1; ix++) {
double du = 0;
double dv = 0;
const int i = ix + iy * L;
du = Du * laplacian(ix, iy, u);
dv = Dv * laplacian(ix, iy, v);
du += calcU(u[i], v[i]);
dv += calcV(u[i], v[i]);
u2[i] = u[i] + du * dt;
v2[i] = v[i] + dv * dt;
}
}
}Gray-Scott系は、最初に「種」を置いておくと、そこから模様が広がっていく系である。なので最初に種を置いておこう。
void init(vd &u, vd &v) {
int d = 3;
for (int i = L / 2 - d; i < L / 2 + d; i++) {
for (int j = L / 2 - d; j < L / 2 + d; j++) {
u[j + i * L] = 0.7;
}
}
d = 6;
for (int i = L / 2 - d; i < L / 2 + d; i++) {
for (int j = L / 2 - d; j < L / 2 + d; j++) {
v[j + i * L] = 0.9;
}
}
}系の中央のuとvに、それぞれ6x6の領域、12x12の初期値を種として置くコードである。
以上を元に、時間発展を行うmain関数はこんな感じになる。
int main() {
const int V = L * L;
vd u(V, 0.0), v(V, 0.0);
vd u2(V, 0.0), v2(V, 0.0);
init(u, v);
for (int i = 0; i < TOTAL_STEP; i++) {
if (i & 1) {
calc(u2, v2, u, v);
} else {
calc(u, v, u2, v2);
}
if (i % INTERVAL == 0) save_as_dat(u);
}
}先程述べたように、偶数時刻と奇数時刻で二本の配列を使い分けているのに注意。
save_as_datは、呼ばれるたびに配列を連番のファイル名で保存する関数である。
全体のコードはこんな感じになる(gs.cpp)。
#include <cstdio>
#include <iostream>
#include <vector>
#include <fstream>
const int L = 128;
const int TOTAL_STEP = 20000;
const int INTERVAL = 200;
const double F = 0.04;
const double k = 0.06075;
const double dt = 0.2;
const double Du = 0.05;
const double Dv = 0.1;
typedef std::vector<double> vd;
void init(vd &u, vd &v) {
int d = 3;
for (int i = L / 2 - d; i < L / 2 + d; i++) {
for (int j = L / 2 - d; j < L / 2 + d; j++) {
u[j + i * L] = 0.7;
}
}
d = 6;
for (int i = L / 2 - d; i < L / 2 + d; i++) {
for (int j = L / 2 - d; j < L / 2 + d; j++) {
v[j + i * L] = 0.9;
}
}
}
double calcU(double tu, double tv) {
return tu * tu * tv - (F + k) * tu;
}
double calcV(double tu, double tv) {
return -tu * tu * tv + F * (1.0 - tv);
}
double laplacian(int ix, int iy, vd &s) {
double ts = 0.0;
ts += s[ix - 1 + iy * L];
ts += s[ix + 1 + iy * L];
ts += s[ix + (iy - 1) * L];
ts += s[ix + (iy + 1) * L];
ts -= 4.0 * s[ix + iy * L];
return ts;
}
void calc(vd &u, vd &v, vd &u2, vd &v2) {
for (int iy = 1; iy < L - 1; iy++) {
for (int ix = 1; ix < L - 1; ix++) {
double du = 0;
double dv = 0;
const int i = ix + iy * L;
du = Du * laplacian(ix, iy, u);
dv = Dv * laplacian(ix, iy, v);
du += calcU(u[i], v[i]);
dv += calcV(u[i], v[i]);
u2[i] = u[i] + du * dt;
v2[i] = v[i] + dv * dt;
}
}
}
void save_as_dat(vd &u) {
static int index = 0;
char filename[256];
sprintf(filename, "conf%03d.dat", index);
std::cout << filename << std::endl;
std::ofstream ofs(filename, std::ios::binary);
ofs.write((char *)(u.data()), sizeof(double)*L * L);
index++;
}
int main() {
const int V = L * L;
vd u(V, 0.0), v(V, 0.0);
vd u2(V, 0.0), v2(V, 0.0);
init(u, v);
for (int i = 0; i < TOTAL_STEP; i++) {
if (i & 1) {
calc(u2, v2, u, v);
} else {
calc(u, v, u2, v2);
}
if (i % INTERVAL == 0) save_as_dat(u);
}
}コンパイル、実行してみよう。
$ g++ -O3 gs.cpp
$ time ./a.out
conf000.dat
conf001.dat
conf002.dat
(snip)
conf097.dat
conf098.dat
conf099.dat
./a.out 1.61s user 0.03s system 96% cpu 1.697 total出てきたデータ(*.dat)は、倍精度実数がL*L個入っている。これをRubyで読み込んでPNG形式で吐く
スクリプトを作っておこう。
require "cairo"
require "pathname"
def convert(datfile)
puts datfile
buf = File.binread(datfile).unpack("d*")
l = Math.sqrt(buf.size).to_i
m = 4
size = l * m
surface = Cairo::ImageSurface.new(Cairo::FORMAT_RGB24, size, size)
context = Cairo::Context.new(surface)
context.set_source_rgb(1, 1, 1)
context.rectangle(0, 0, size, size)
context.fill
l.times do |x|
l.times do |y|
u = buf[x + y * l]
context.set_source_rgb(0, u, 0)
context.rectangle(x * m, y * m, m, m)
context.fill
end
end
pngfile = Pathname(datfile).sub_ext(".png").to_s
surface.write_to_png(pngfile)
end
`ls *.dat`.split(/\n/).each do |f|
convert(f)
endこれで一括で処理する。
$ ruby image.rb
conf000.dat
conf001.dat
conf002.dat
(snip)
conf097.dat
conf098.dat
conf099.datするとこんな感じの画像が得られる。
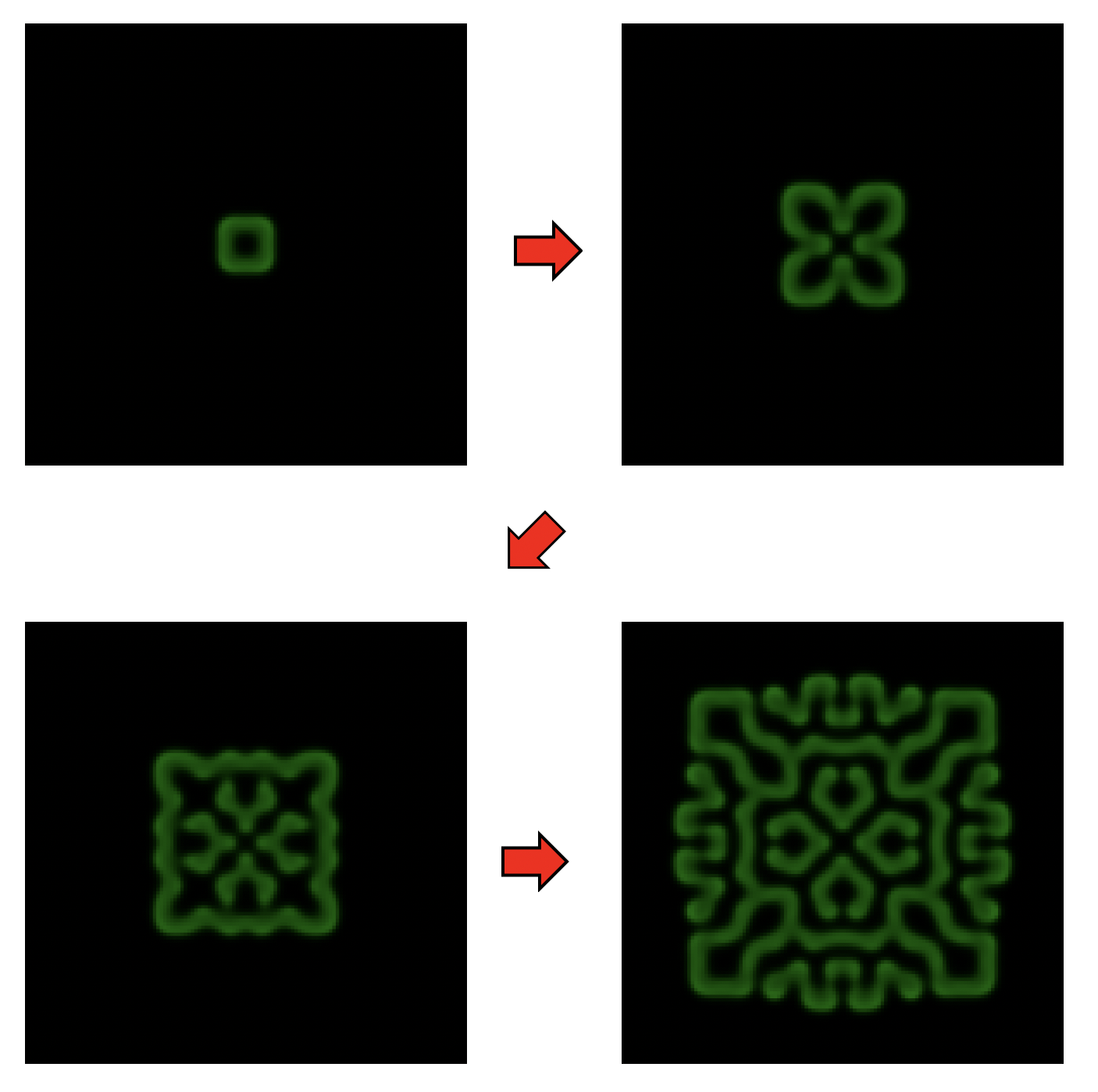
並列化ステップ1: 通信の準備など
さて、さっそく反応拡散方程式を二次元領域分割により並列化していくわけだが、 並列化で重要なのは、 いきなり本番コードで通信アルゴリズムを試さない ということである。 まずは、今やろうとしている通信と同じアルゴリズムだけを抜き出したコードを書き、ちゃんと想定通りに通信できていることを確かめる。 実際のデータは倍精度実数だが、とりあえず整数データでいろいろためそう。
まず、通信関連のコードを書く前に、領域分割により、全体をどうやって分割するか、 各プロセスはどこを担当するかといった基本的なセットアップを確認しよう。
いま、LxLのグリッドがあるとしよう。これをprocsプロセスで分割する。
この時、なるべく「のりしろ」が小さくなるように分割したい。
例えば4プロセスなら2x2に、24プロセスなら6x4という具合である。
このためには、与えられたプロセス数を、なるべく似たような数字になるように
因数分解してやらないといけない。
MPIにはそのための関数、MPI_Dims_createが用意されている。
使い方は、二次元分割なら、procsにプロセス数が入っているとして、
int d2[2] = {};
MPI_Dims_create(procs, 2, d2);のように呼ぶと、d2[0]とd2[1]に分割数が入ってくる。三次元分割をしたければ、
int d3[3] = {};
MPI_Dims_create(procs, 3, d3);などと、分割数3を指定し、3要素の配列を食わせてやれば良い。
ただし、OpenMPIのMPI_Dims_createは若干動作が怪しいので注意すること。
例えば9プロセスを二次元分割したら3x3になってほしいが、9x1を返してくる。
Intel MPIやSGI
MPTはちゃんと3x3を返してくるので、このあたりは実装依存のようだ。
気になる場合は自分で因数分解コードを書いて欲しい。
さて、procsプロセスを、GX*GYと分割することにしよう。 すると、各プロセスは、横がL/GX、縦がL/GY個のサイトを保持すれば良い。 例えば8x8の系を4プロセスで並列化する際、一つのプロセスが担当するのは4x4となるが、 上下左右に1列余分に必要になるので、合わせて6x6のデータを保持することになる。
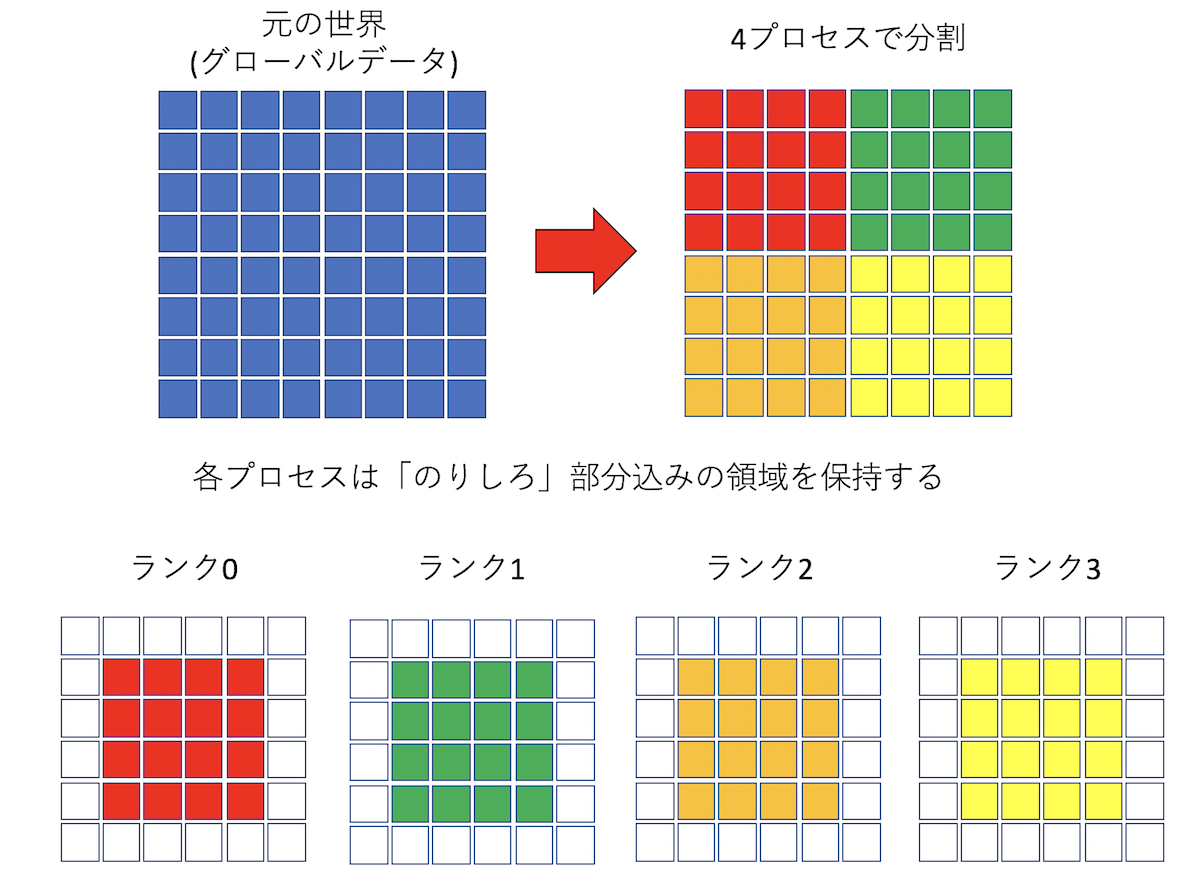
また、各プロセスは自分がどの場所を担当しているかも知っておきたいし、担当する領域のサイズも保持しておきたい。
これらに加えてランクや総プロセス数といった並列化情報を、MPIinfoという構造体にまとめて突っ込んで置こう。
とりあえず必要な情報はこんな感じだろうか。
struct MPIinfo {
int rank; //ランク番号
int procs; //総プロセス数
int GX, GY; // プロセスをどう分割したか (GX*GY=procs)
int local_grid_x, local_grid_y; // 自分が担当する位置
int local_size_x, local_size_y; // 自分が担当する領域のサイズ(のりしろ含まず)
};MPIinfoの各値をセットする関数、setup_infoを作っておこう。こんな感じかな。
void setup_info(MPIinfo &mi) {
int rank = 0;
int procs = 0;
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &procs);
int d2[2] = {};
MPI_Dims_create(procs, 2, d2);
mi.rank = rank;
mi.procs = procs;
mi.GX = d2[0];
mi.GY = d2[1];
mi.local_grid_x = rank % mi.GX;
mi.local_grid_y = rank / mi.GX;
mi.local_size_x = L / mi.GX;
mi.local_size_y = L / mi.GY;
}自分が保持するデータをstd::vector<int> local_dataとして宣言しよう。のりしろの部分も考慮するとこんな感じになる。
MPIinfo mi;
setup_info(mi);
std::vector<int> local_data((mi.local_size_x + 2) * (mi.local_size_y + 2), 0);あとの通信がうまくいっているか確認するため、ローカルデータに「のりしろ」以外に通し番号を降っておこう。 例えばL=8で、procs = 4の場合に、各プロセスにこういうデータを保持させたい。
rank = 0
000 000 000 000 000 000
000 000 001 002 003 000
000 004 005 006 007 000
000 008 009 010 011 000
000 012 013 014 015 000
000 000 000 000 000 000
rank = 1
000 000 000 000 000 000
000 016 017 018 019 000
000 020 021 022 023 000
000 024 025 026 027 000
000 028 029 030 031 000
000 000 000 000 000 000
rank = 2
000 000 000 000 000 000
000 032 033 034 035 000
000 036 037 038 039 000
000 040 041 042 043 000
000 044 045 046 047 000
000 000 000 000 000 000
rank = 3
000 000 000 000 000 000
000 048 049 050 051 000
000 052 053 054 055 000
000 056 057 058 059 000
000 060 061 062 063 000
000 000 000 000 000 000このような初期化をする関数initを用意する。
void init(std::vector<int> &local_data, MPIinfo &mi) {
const int offset = mi.local_size_x * mi.local_size_y * mi.rank;
for (int iy = 0; iy < mi.local_size_y; iy++) {
for (int ix = 0; ix < mi.local_size_x; ix++) {
int index = (ix + 1) + (iy + 1) * (mi.local_size_x + 2);
int value = ix + iy * mi.local_size_x + offset;
local_data[index] = value;
}
}
}自分が担当する領域の左上に来る番号をoffsetとして計算し、そこから通し番号を降っているだけである。
このローカルなデータをダンプする関数も作っておく。
void dump_local_sub(std::vector<int> &local_data, MPIinfo &mi) {
printf("rank = %d\n", mi.rank);
for (int iy = 0; iy < mi.local_size_y + 2; iy++) {
for (int ix = 0; ix < mi.local_size_x + 2; ix++) {
unsigned int index = ix + iy * (mi.local_size_x + 2);
printf("%03d ", local_data[index]);
}
printf("\n");
}
printf("\n");
}dump_local_subに自分が保持するstd::vectorを渡せば表示されるのだが、
複数のプロセスから一気に標準出力に吐くと表示が乱れる可能性がある。
各プロセスからファイルに吐いてしまっても良いが、こういう時は、プロセスの数だけループをまわし、ループカウンタが自分のランク番号と同じになった時に書き込む、
というコードが便利である。全プロセスが順番待ちをするので速度は遅いが、主にデバッグに使うので問題ない。
こんな感じである。
void dump_local(std::vector<int> &local_data, MPIinfo &mi) {
for (int i = 0; i < mi.procs; i++) {
MPI_Barrier(MPI_COMM_WORLD);
if (i == mi.rank) {
dump_local_sub(local_data, mi);
}
}
}毎回バリア同期が必要なことに注意。この、
for (int i = 0; i < procs; i++) {
MPI_Barrier(MPI_COMM_WORLD);
if (i == rank) {
do_something();
}
}というイディオムは、MPIで頻出するので覚えておくと良いかもしれない。
4プロセス実行し、dump_localを呼ぶと、先程の「のりしろ付きのローカルデータ」がダンプされる。
並列化ステップ2: データの保存
計算を実行するにあたり、必要な通信は、
- 時間発展のための「のりしろ」の通信
- 計算の途中経過のデータの保存のための集団通信
の二種類である。一次元分割の時と同様に、まずは後者、データの保存のための通信を考えよう。
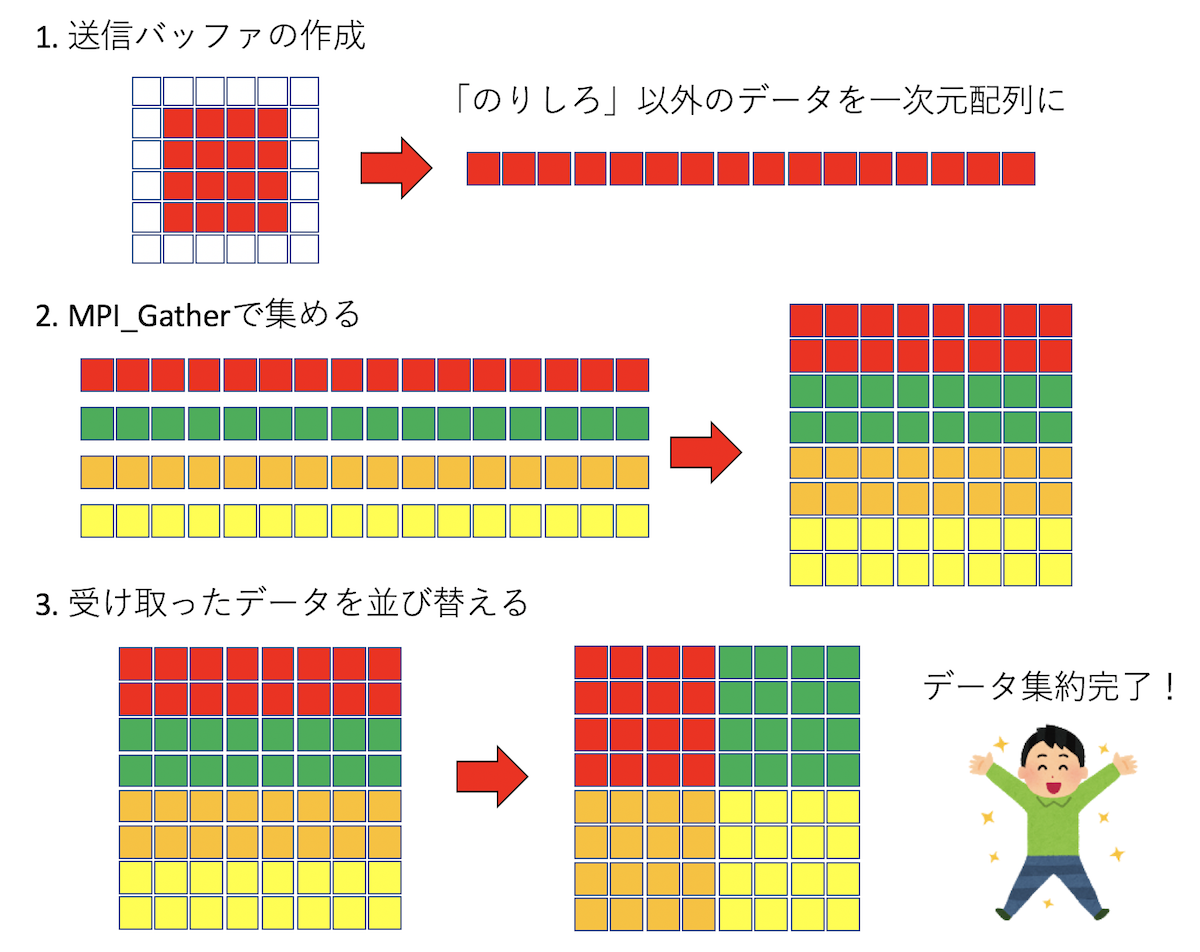
時間発展した結果を保存したいので、各プロセスが保持するデータを集約したい。
各プロセスが保持するデータをローカルデータ、系全体のデータをグローバルデータと呼ぶことにする。
「のりしろ」は計算の時には必要だが、データの保存の時には不要だ。
なので、各プロセスはまず、ローカルデータから「のりしろ」を除いたデータを用意し、
それをMPI_Gatherを使ってルートプロセスに集める。
今、各プロセスがこんな感じにデータを持っていたとする。
rank = 0
000 000 000 000 000 000
000 000 001 002 003 000
000 004 005 006 007 000
000 008 009 010 011 000
000 012 013 014 015 000
000 000 000 000 000 000
rank = 1
000 000 000 000 000 000
000 016 017 018 019 000
000 020 021 022 023 000
000 024 025 026 027 000
000 028 029 030 031 000
000 000 000 000 000 000
rank = 2
000 000 000 000 000 000
000 032 033 034 035 000
000 036 037 038 039 000
000 040 041 042 043 000
000 044 045 046 047 000
000 000 000 000 000 000
rank = 3
000 000 000 000 000 000
000 048 049 050 051 000
000 052 053 054 055 000
000 056 057 058 059 000
000 060 061 062 063 000
000 000 000 000 000 000000は「のりしろ」である。グローバル領域は二次元的に分割されるが、各プロセスはそれを一次元的に保持しているので、「のりしろ」を除いてデータをコピーするところを除けば、通信部分は一次元の時と同じになる。
void gather(std::vector<int> &local_data, MPIinfo &mi) {
const int lx = mi.local_size_x;
const int ly = mi.local_size_y;
std::vector<int> sendbuf(lx * ly);
// 「のりしろ」を除いたデータのコピー
for (int iy = 0; iy < ly; iy++) {
for (int ix = 0; ix < lx; ix++) {
int index_from = (ix + 1) + (iy + 1) * (lx + 2);
int index_to = ix + iy * lx;
sendbuf[index_to] = local_data[index_from];
}
}
std::vector<int> recvbuf;
if (mi.rank == 0) {
recvbuf.resize(lx * ly * mi.procs);
}
MPI_Gather(sendbuf.data(), lx * ly, MPI_INT, recvbuf.data(), lx * ly, MPI_INT, 0, MPI_COMM_WORLD);
// ここで、ランク0番のプロセスの保持するrecvbufにグローバルデータが入る。
}しかし、このようにして集約されたグローバルデータは、各プロセスが論理的に保持するデータと場所が異なり、こんな感じになる。
Before reordering
000 001 002 003 004 005 006 007
008 009 010 011 012 013 014 015
016 017 018 019 020 021 022 023
024 025 026 027 028 029 030 031
032 033 034 035 036 037 038 039
040 041 042 043 044 045 046 047
048 049 050 051 052 053 054 055
056 057 058 059 060 061 062 063数字が連番になっているのがわかるだろうか。デバッグに便利なように、そうなるようにローカルデータに数字を振っておいた。 さて、論理的にはこういう配置になっていて欲しい。
After reordering
000 001 002 003 016 017 018 019
004 005 006 007 020 021 022 023
008 009 010 011 024 025 026 027
012 013 014 015 028 029 030 031
032 033 034 035 048 049 050 051
036 037 038 039 052 053 054 055
040 041 042 043 056 057 058 059
044 045 046 047 060 061 062 063というわけで、そうなるようにデータを並び替えればよい。並び替えのための関数reorderingはこう書けるだろう。
void reordering(std::vector<int> &v, MPIinfo &mi) {
std::vector<int> v2(v.size());
std::copy(v.begin(), v.end(), v2.begin());
const int lx = mi.local_size_x;
const int ly = mi.local_size_y;
int i = 0;
for (int r = 0; r < mi.procs; r++) {
int rx = r % mi.GX;
int ry = r / mi.GX;
int sx = rx * lx;
int sy = ry * ly;
for (int iy = 0; iy < ly; iy++) {
for (int ix = 0; ix < lx; ix++) {
int index = (sx + ix) + (sy + iy) * L;
v[index] = v2[i];
i++;
}
}
}
}以上の処理まで含めて、gather完成である。
void gather(std::vector<int> &local_data, MPIinfo &mi) {
const int lx = mi.local_size_x;
const int ly = mi.local_size_y;
std::vector<int> sendbuf(lx * ly);
// 「のりしろ」を除いたデータのコピー
for (int iy = 0; iy < ly; iy++) {
for (int ix = 0; ix < lx; ix++) {
int index_from = (ix + 1) + (iy + 1) * (lx + 2);
int index_to = ix + iy * lx;
sendbuf[index_to] = local_data[index_from];
}
}
std::vector<int> recvbuf;
if (mi.rank == 0) {
recvbuf.resize(lx * ly * mi.procs);
}
MPI_Gather(sendbuf.data(), lx * ly, MPI_INT, recvbuf.data(), lx * ly, MPI_INT, 0, MPI_COMM_WORLD);
if (mi.rank == 0) {
printf("Before reordering\n");
dump_global(recvbuf);
reordering(recvbuf, mi);
printf("After reordering\n");
dump_global(recvbuf);
}
}送信前や送信後にデータの処理が必要となるので、やってることが単純なわりにコード量がそこそこの長さになる。 このあたりが「MPIは面倒くさい」と言われる所以かもしれない。筆者も「MPIは面倒くさい」ことは否定しない。 しかし、ここまで読んでくださった方なら「MPIは難しくはない」ということも同意してもらえると思う。 MPIは書いた通りに動く。なので、通信アルゴリズムが決まっていれば、その手順どおりに書くだけである。 実際面倒なのは通信そのものよりも、通信の前処理と後処理だったりする(そもそも今回も通信は一行だけだ)。
以上をすべてまとめたコードをgather2d.cppとしよう。やや大きいので、ウェブへのリンクを貼っておく。
https://github.com/kaityo256/sevendayshpc/blob/master/day5/gather2d.cpp
main関数だけ書いておくとこんな感じ。
int main(int argc, char **argv) {
MPI_Init(&argc, &argv);
MPIinfo mi;
setup_info(mi);
// ローカルデータの確保
std::vector<int> local_data((mi.local_size_x + 2) * (mi.local_size_y + 2), 0);
// ローカルデータの初期化
init(local_data, mi);
// ローカルデータの表示
dump_local(local_data, mi);
// ローカルデータを集約してグローバルデータに
gather(local_data, mi);
MPI_Finalize();
}まぁ、そのまんま手続きを書いただけですね。
並列化ステップ2: のりしろの通信
さて、計算を実行するためには、上下左右のプロセスから自分の「のりしろ」に情報を受け取らないといけない。 問題は、二次元の場合には角の情報、つまり「斜め方向」の通信も必要なことである。 普通に考えると、左右2回、上下2回、角4つで8回の通信が必要となるのだが、左右から受け取ったデータを、上下に転送することで、4回の通信で斜め方向の通信も完了する。
どうでも良いが筆者は昔ブログを書いており(今は書いてないが)、「斜め方向の通信どうするかなぁ」と書いたら、日記の読者二人から別々にこのアルゴリズムを教えていただいた(その節はありがとうございます)。ブログも書いてみるものである。
データの転送を図解するとこんな感じになる。まず、左右方向の通信。実際の例では2x2分割のため、自分から見て左にいるプロセスと右にいるプロセスが同一になってしまうが、図では別プロセスとして描いているから注意。
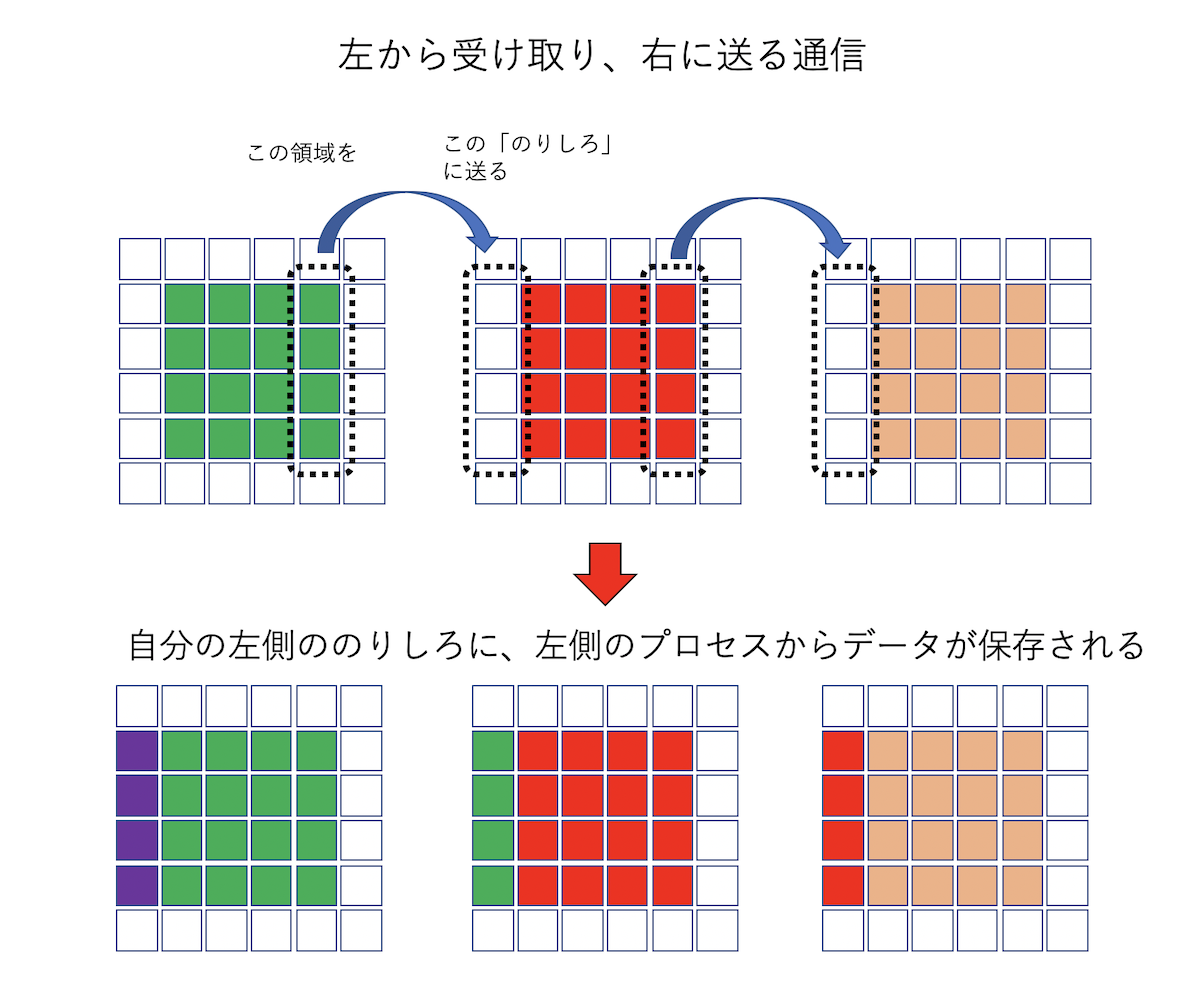
左右の通信が終わったら、左右からもらったデータも込みで上下に転送する。以下は、「下から受け取り、上に送る」通信。
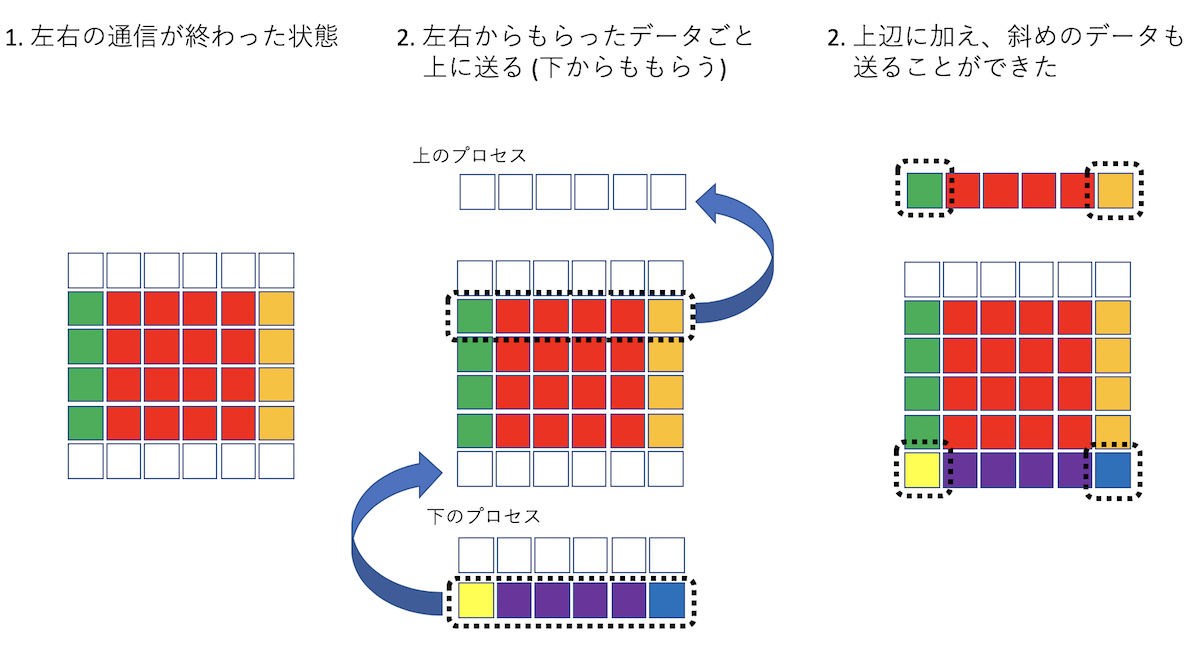
最後の点線で囲ったデータが「斜め方向のプロセスが保持していたデータ」であり、間接的に受け取ったことになる。
まず、上下左右にいるプロセス番号を知りたい。MPIinfoにget_rankメソッドを追加しておこう。
struct MPIinfo {
int rank;
int procs;
int GX, GY;
int local_grid_x, local_grid_y;
int local_size_x, local_size_y;
// 自分から見て(dx,dy)だけずれたプロセスのrankを返す
int get_rank(int dx, int dy) {
int rx = (local_grid_x + dx + GX) % GX;
int ry = (local_grid_y + dy + GY) % GY;
return rx + ry * GX;
}
};これを使って、左右(x方向)に通信して、右と左の「のりしろ」データを交換するコードはこんな感じに書ける。
void sendrecv_x(std::vector<int> &local_data, MPIinfo &mi) {
const int lx = mi.local_size_x;
const int ly = mi.local_size_y;
std::vector<int> sendbuf(ly);
std::vector<int> recvbuf(ly);
int left = mi.get_rank(-1, 0);
int right = mi.get_rank(1, 0);
for (int i = 0; i < ly; i++) {
int index = lx + (i + 1) * (lx + 2);
sendbuf[i] = local_data[index];
}
MPI_Status st;
MPI_Sendrecv(sendbuf.data(), ly, MPI_INT, right, 0,
recvbuf.data(), ly, MPI_INT, left, 0, MPI_COMM_WORLD, &st);
for (int i = 0; i < ly; i++) {
int index = (i + 1) * (lx + 2);
local_data[index] = recvbuf[i];
}
for (int i = 0; i < ly; i++) {
int index = 1 + (i + 1) * (lx + 2);
sendbuf[i] = local_data[index];
}
MPI_Sendrecv(sendbuf.data(), ly, MPI_INT, left, 0,
recvbuf.data(), ly, MPI_INT, right, 0, MPI_COMM_WORLD, &st);
for (int i = 0; i < ly; i++) {
int index = lx + 1 + (i + 1) * (lx + 2);
local_data[index] = recvbuf[i];
}
}全く同様にy方向の通信も書けるが、先に述べたように「左右からもらったデータも転送」するため、その分がちょっとだけ異なる。
このアルゴリズムを実装するとこんな感じになる。
https://github.com/kaityo256/sevendayshpc/blob/master/day5/sendrecv.cpp
実行結果はこんな感じ。
$ mpic++ sendrecv.cpp
$ mpirun -np 4 ./a.out
# 通信前
rank = 0
000 000 000 000 000 000
000 000 001 002 003 000
000 004 005 006 007 000
000 008 009 010 011 000
000 012 013 014 015 000
000 000 000 000 000 000
rank = 1
000 000 000 000 000 000
000 016 017 018 019 000
000 020 021 022 023 000
000 024 025 026 027 000
000 028 029 030 031 000
000 000 000 000 000 000
rank = 2
000 000 000 000 000 000
000 032 033 034 035 000
000 036 037 038 039 000
000 040 041 042 043 000
000 044 045 046 047 000
000 000 000 000 000 000
rank = 3
000 000 000 000 000 000
000 048 049 050 051 000
000 052 053 054 055 000
000 056 057 058 059 000
000 060 061 062 063 000
000 000 000 000 000 000
# 左右の通信終了後
rank = 0
000 000 000 000 000 000
019 000 001 002 003 016
023 004 005 006 007 020
027 008 009 010 011 024
031 012 013 014 015 028
000 000 000 000 000 000
rank = 1
000 000 000 000 000 000
003 016 017 018 019 000
007 020 021 022 023 004
011 024 025 026 027 008
015 028 029 030 031 012
000 000 000 000 000 000
rank = 2
000 000 000 000 000 000
051 032 033 034 035 048
055 036 037 038 039 052
059 040 041 042 043 056
063 044 045 046 047 060
000 000 000 000 000 000
rank = 3
000 000 000 000 000 000
035 048 049 050 051 032
039 052 053 054 055 036
043 056 057 058 059 040
047 060 061 062 063 044
000 000 000 000 000 000
# 上下の通信終了後 (これで斜め方向も完了)
rank = 0
063 044 045 046 047 060
019 000 001 002 003 016
023 004 005 006 007 020
027 008 009 010 011 024
031 012 013 014 015 028
051 032 033 034 035 048
rank = 1
047 060 061 062 063 044
003 016 017 018 019 000
007 020 021 022 023 004
011 024 025 026 027 008
015 028 029 030 031 012
035 048 049 050 051 032
rank = 2
031 012 013 014 015 028
051 032 033 034 035 048
055 036 037 038 039 052
059 040 041 042 043 056
063 044 045 046 047 060
019 000 001 002 003 016
rank = 3
015 028 029 030 031 012
035 048 049 050 051 032
039 052 053 054 055 036
043 056 057 058 059 040
047 060 061 062 063 044
003 016 017 018 019 000先の図と比べて、正しく通信が行われていることを確認してほしい。
結局、通信プログラムとはこういうことをする。
- 送信バッファと受信バッファを用意する
- 送信バッファに送るべきデータをコピー
- 通信する
- 受信バッファに来たデータを必要な場所にコピー
通信そのものは関数呼び出し一発で難しくも面倒でもないが、送受信バッファの作業が面倒くさい。
並列化ステップ3: 並列コードの実装
通信に使うアルゴリズムの確認が終わったので、いよいよ差分法コードに実装してみよう。まず、初期化の部分を考えないといけない。初期化についてはグローバル座標で考えたいが、実際に値を入れるのは各プロセスが保持するローカルデータである。そこで、「このグローバル座標が自分の領域に含まれるか?」「含まれるなら、そのインデックスはどこか?」が知りたくなる。それをMPIinfoのメソッドとして追加しておこう。
struct MPIinfo {
int rank;
int procs;
int GX, GY;
int local_grid_x, local_grid_y;
int local_size_x, local_size_y;
// 自分から見て +dx, +dyだけずれたプロセスのランクを返す
int get_rank(int dx, int dy) {
int rx = (local_grid_x + dx + GX) % GX;
int ry = (local_grid_y + dy + GY) % GY;
return rx + ry * GX;
}
// 自分の領域に含まれるか
bool is_inside(int x, int y) {
int sx = local_size_x * local_grid_x;
int sy = local_size_y * local_grid_y;
int ex = sx + local_size_x;
int ey = sy + local_size_y;
if (x < sx)return false;
if (x >= ex)return false;
if (y < sy)return false;
if (y >= ey)return false;
return true;
}
// グローバル座標をローカルインデックスに
int g2i(int gx, int gy) {
int sx = local_size_x * local_grid_x;
int sy = local_size_y * local_grid_y;
int x = gx - sx;
int y = gy - sy;
return (x + 1) + (y + 1) * (local_size_x + 2);
}
};そうすると、初期化処理はこんな感じにかける。
void init(vd &u, vd &v, MPIinfo &mi) {
int d = 3;
for (int i = L / 2 - d; i < L / 2 + d; i++) {
for (int j = L / 2 - d; j < L / 2 + d; j++) {
if (!mi.is_inside(i, j)) continue;
int k = mi.g2i(i, j);
u[k] = 0.7;
}
}
d = 6;
for (int i = L / 2 - d; i < L / 2 + d; i++) {
for (int j = L / 2 - d; j < L / 2 + d; j++) {
if (!mi.is_inside(i, j)) continue;
int k = mi.g2i(i, j);
v[k] = 0.9;
}
}
}要するにグローバル座標でループを回してしまって、自分の領域に入っていたら(mi.is_inside(i, j)==true)、ローカルインデックスを取得して、そこに値を書き込む、というだけのコードである。自分の守備範囲外もループが回って非効率に思えるかもしれないが、どうせ初期化処理は最初に一度しか走らないし、こうしておくと他の初期化をしたい時や、ファイルから読み込む時に、シリアルコードと並列コードで同じファイルが使えたりして便利である。
初期化処理が済んだら、可視化用のファイル保存コードを書こう。といっても、ステップ2で書いたコードをintからdoubleに変えて、標準出力にダンプしていたのをファイルに保存するだけである。
// 各プロセスから保存用のデータを受け取ってセーブ
void save_as_dat_mpi(vd &local_data, MPIinfo &mi) {
const int lx = mi.local_size_x;
const int ly = mi.local_size_y;
vd sendbuf(lx * ly);
// 「のりしろ」を除いたデータのコピー
for (int iy = 0; iy < ly; iy++) {
for (int ix = 0; ix < lx; ix++) {
int index_from = (ix + 1) + (iy + 1) * (lx + 2);
int index_to = ix + iy * lx;
sendbuf[index_to] = local_data[index_from];
}
}
vd recvbuf;
if (mi.rank == 0) {
recvbuf.resize(lx * ly * mi.procs);
}
MPI_Gather(sendbuf.data(), lx * ly, MPI_DOUBLE, recvbuf.data(), lx * ly, MPI_DOUBLE, 0, MPI_COMM_WORLD);
if (mi.rank == 0) {
reordering(recvbuf, mi);
save_as_dat(recvbuf);
}
}データの再配置(reordering)もほとんど同じなので割愛。ここで、
いきなり時間発展させずに
初期化処理をしてからファイルに保存し、正しく初期化、保存できているか確認しておこう。
「のりしろ」の通信部分も、基本的にintをdoubleに変更するだけなので割愛。ただし、uとvの両方を通信しないといけないので、それをまとめて行う関数を作っておこう。
void sendrecv(vd &u, vd &v, MPIinfo &mi) {
sendrecv_x(u, mi);
sendrecv_y(u, mi);
sendrecv_x(v, mi);
sendrecv_y(v, mi);
}これを時間発展直前に呼び出せば、「のりしろ」部分の通信が完了している。 ここでも、いきなり時間発展させずに 初期化処理を行った後に「のりしろ通信」を行い、ローカルデータをダンプして正しく通信できているか確認しよう。
そこまでできればあとはシリアル版とほぼ同じ。main関数はこんな感じになる。
int main(int argc, char **argv) {
MPI_Init(&argc, &argv);
MPIinfo mi;
setup_info(mi);
const int V = (mi.local_size_x + 2) * (mi.local_size_y + 2);
vd u(V, 0.0), v(V, 0.0);
vd u2(V, 0.0), v2(V, 0.0);
init(u, v, mi);
for (int i = 0; i < TOTAL_STEP; i++) {
if (i & 1) {
sendrecv(u2, v2, mi);
calc(u2, v2, u, v, mi);
} else {
sendrecv(u, v, mi);
calc(u, v, u2, v2, mi);
}
if (i % INTERVAL == 0) save_as_dat_mpi(u, mi);
}
MPI_Finalize();
}MPIの初期化、終了処理、および計算の直前に通信を呼んでるところ以外はシリアル版と変わらないことがわかる。
実行してみよう。普通のmpic++を使ってしまうとclang++が呼ばれてしまう。先程、g++でコンパイルしたシリアル版と実行時間を比較するため、明示的にg++でコンパイルして実行しよう。筆者の環境ではMPIのヘッダやライブラリにパスが通っているので、-lmpi -lmpi_cxxをつけるだけでコンパイルできる。
$ g++ -O3 gs_mpi.cpp -lmpi -lmpi_cxx
$ time mpirun -np 4 --oversubscribe ./a.out
conf000.dat
conf001.dat
conf002.dat
(snip)
conf098.dat
conf099.dat
mpirun -np 4 --oversubscribe ./a.out 2.39s user 0.29s system 321% cpu 0.832 totaltimeコマンドで出てくる%は、どれだけCPUコアを使ったかを表している。一つのCPUコアを使い切ると100%になる。ここでは321%と表示されているため、4コアを使った並列計算ができていることがわかる。実行時間も1.697s→0.832sと倍近く早くなっている。
シリアル版をserial、MPI版をmpiというディレクトリで実行し、それぞれにデータファイルがあるとして、diffで確認してみよう。時間発展前する前は当然同じ結果になる。
$ diff -s serial/conf000.dat mpi/conf000.dat
Files serial/conf000.dat and mpi/conf000.dat are identicalしかし、誤差の関係で、次のステップから結果がずれていく。
$ diff -s serial/conf001.dat mpi/conf001.dat
Binary files serial/conf001.dat and mpi/conf001.dat differこれは、シリアル版とMPI版で加算の順序が変わることによる。しかし、本質的には同じ計算をしているので、可視化すると同じような図が出てくるはずである。見てみよう。
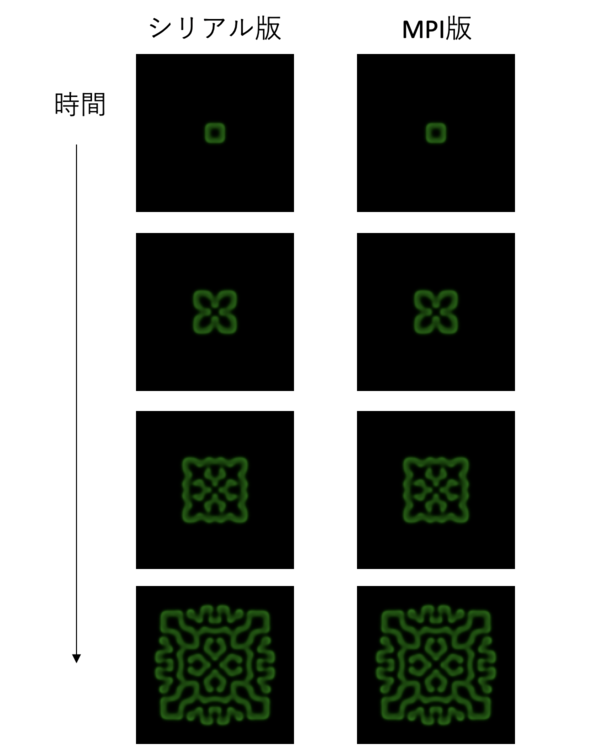
うん、大丈夫そうですね。
さて、実行時間は1.697s→0.832sと2倍近くなったが、使ったCPUコアは4コアであった。つまり、理想的には4倍早くなって欲しいのに、2倍近くしか早くなっていない。並列化効率は50%程度である。
ん?並列化効率が物足りない? そういう時はウィースケーリングに逃げてサイズで殴る。
というわけでサイズをでかくする。一辺4倍にして再度実行してみよう。
-const int L = 128;
+const int L = 512;$ g++ -O3 gs.cpp
$ time ./a.out
(snip)
./a.out 57.98s user 0.16s system 99% cpu 58.248 total
$ g++ -O3 gs_mpi.cpp -lmpi -lmpi_cxx
$ time mpirun -np 4 --oversubscribe ./a.out
./a.out 57.98s user 0.16s system 99% cpu 58.248 total
mpirun -np 4 --oversubscribe ./a.out 68.28s user 1.72s system 382% cpu 18.305 total実行時間が58.248s → 18.305となり、並列化効率も80%近くに向上した。それでもなんか文句を言ってくる人がいたら、とてもローカルPCのメモリには乗りきらないほど大きな系を計算して黙らせよう。「並列化効率で悩んだらサイズに逃げろ」と覚えておくと良い。
余談:MPIの面倒くささ
本格的な領域分割コードの例として、二次元反応拡散方程式を並列化してみた。「並列化」によってどれくらいコードが増えたか見てみよう。
$ wc gs.cpp gs_mpi.cpp
89 430 1969 gs.cpp
272 1271 7345 gs_mpi.cpp
361 1701 9314 totalというわけで、89行から272行になった。3倍増である。つまり、もともとの計算コードの二倍の量の通信コードがついたことになる。といっても、「通信コードそのもの」の量は大したことがない。
$ grep MPI_ gs_mpi.cpp
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &procs);
MPI_Dims_create(procs, 2, d2);
MPI_Gather(sendbuf.data(), lx * ly, MPI_DOUBLE, recvbuf.data(), lx * ly, MPI_DOUBLE, 0, MPI_COMM_WORLD);
MPI_Status st;
MPI_Sendrecv(sendbuf.data(), ly, MPI_DOUBLE, right, 0,
recvbuf.data(), ly, MPI_DOUBLE, left, 0, MPI_COMM_WORLD, &st);
MPI_Sendrecv(sendbuf.data(), ly, MPI_DOUBLE, left, 0,
recvbuf.data(), ly, MPI_DOUBLE, right, 0, MPI_COMM_WORLD, &st);
MPI_Status st;
MPI_Sendrecv(sendbuf.data(), lx + 2, MPI_DOUBLE, up, 0,
recvbuf.data(), lx + 2, MPI_DOUBLE, down, 0, MPI_COMM_WORLD, &st);
MPI_Sendrecv(sendbuf.data(), lx + 2, MPI_DOUBLE, down, 0,
recvbuf.data(), lx + 2, MPI_DOUBLE, up, 0, MPI_COMM_WORLD, &st);
MPI_Init(&argc, &argv);
MPI_Finalize();
$ grep MPI_ gs_mpi.cpp | wc
16 82 850MPI_Status stの宣言を除くと14行だけである。それ以外はバッファの準備と整理に費やされている。
これをもって「MPIは面倒くさい」というのであれば、私は同意する。しかし、「MPIの面倒くささ」の本質はそこではないように思う。
MPIを使って並列コードを書くことを「並列化 (parallelization)」と呼ぶ。「並列化」という言葉から想像されるのは、「もともとあるシリアル版のコードを改造して並列コードを書く」という作業であろう。典型的には、
- シリアルコードを書く
- 大きな系がやりたくなったので、OpenMPを使ってスレッド並列をする
- さらにMPIを使って並列版に修正する
といった開発プロセスとなりがちなのだと思われる。しかし、既存のコードを修正してMPIを入れていく作業は極めて面倒くさく、バグが入りやすく、かつやっている最中に何をやってるかわからなくなりがちである。一度何をやってるかわからない状態になったら、もうどこがバグなのか、バグが何に起因するのかわからず、泥沼にハマっていく。筆者は、学生さんだけでなくプログラムで飯を食っているプロな人でもそういう状態になっているのを何度も目撃している。
さて、スレッド並列はともかく、MPIを使った並列化とは、MPI向けに新規にコードを書き直す作業である。「正しい」並列化プロセスは以下の通りとなる。
- シリアルコードを書く
- MPI並列化に必要な通信パターンを抽出する
- その通信パターンだけを抜き出してテストコードを書く
- シリアルコードとテストコードを参照しながら、新規にコードを開発する
具体的に4つ目のプロセスでは、「初期化してgatherして保存し、正しいことを確認」「初期化後にのりしろ通信して、正しいことを確認」してから、次のステップに進んでいる。並列版として開発したgs_mpi.cppは、シリアル版であるgs.cppをコピーせず、gs.cppを参照しながらゼロから開発していった。MPIは面倒である。その感覚は正しい。しかし、順を追って開発していけば、別に難しくはない。ソースコードが三倍になった、というと「うっ」と思うかもしれないが、それでも300行も無いのだし、通信コードを書くこと自体は対して時間はかからない。並列化に限ったことではないが、プログラムの開発時間のほとんどはデバッグでしめられている。面倒臭がらずに、通信ロジックのテストコードなどをきちんと書いていけば、さほど時間はかからずに並列化することができるだろう。
もし2万行のソースコードを渡されて「並列化しろ」と言われたら?それはもうご愁傷様としか……