Barnes-Hut treeの構築 (分布数えソート版)
Barnes-Hut treeの構築 (分布数えソート版)
はじめに
わけあって、重力多体系の計算で使われるBarnes-Hut treeを構築することになったので覚書の続き。前回はinsertion版だが、今回は分布数えソート(counting sort)版。
コードは https://github.com/kaityo256/barnes-hut に置いてあるソースのうちbarnes-hut-counting.rbがそれ。
Barnes-Hut treeとは
空間を再帰的に分割していって、各領域にたかだか一個までしか粒子が入らないようにしたい。(以下略)
要するにこういう入力にたいして、

こういう出力が欲しい。
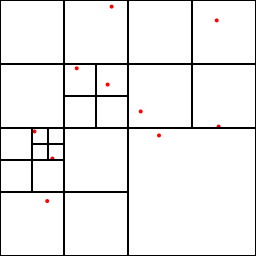
アルゴリズム
前回は、粒子をルートノードに追加依頼すると、適当な子ノードを作成しつつ、よしなに空間を分割してくれる方法を考えた。今度は一度にノードに粒子のインデックスを渡し、それを各子ノードにまとめて分配していく方法を採用する。1
まず、256×256の空間に、以下のような粒子座標が入力として与えられたとする。
0 111.61469494835296 6.637115347940181
1 140.71359433694954 111.44253251027888
2 107.61415733439719 84.56571417699178
3 52.39005031368768 158.5333673857699
4 76.71159646067792 68.30778242633386
5 159.0102611889395 135.460376134922
6 34.45246600830299 131.47599904403108
7 47.21660560561031 201.0457978410684
8 218.61767491570913 126.52463036977352
9 216.7197402515118 20.389242114319615
それぞれ粒子番号、x座標、y座標である。これらが、空間を4分割した時にどこに入るかを考えると、空間の一辺の長さの半分(128)で割って小数点以下切り捨てたものをインデックスとすれば良い。例えば、分割した部分空間を以下のように番号付けする。

すると、先程の座標リストは、それぞれ以下のようなインデックスになる。
0 0
1 1
2 0
3 2
4 0
5 3
6 2
7 2
8 1
9 1
それぞれ粒子番号、空間インデックスである。これを、空間インデックスでソートする。空間インデックスは4種類しかないので、分布数えソート(counting sort)が使える。するとこうなる。
0 0
2 0
4 0
1 1
8 1
9 1
3 2
6 2
7 2
5 3
ソート後、「0」に属す粒子だけ空間インデックス0番を担当する子ノードに、「1」に属す粒子だけ1番を担当する子ノードに・・・と再帰的に渡してやれば分割完了である。
実装
先程のアルゴリズムを実装したノードクラスNodeはこんな感じになるだろう。
class Node
def initialize(size, x, y)
@size = size
@x = x
@y = y
@nodes = []
end
def divide(s, len, index, q)
return if len <=1
temp = index[s,len]
count = Array.new(4) {0}
hs = @size*0.5
temp.each do |i|
ix = ((q[i].x - @x)/hs).to_i
iy = ((q[i].y - @y)/hs).to_i
id = ix + iy * 2
count[id] = count[id] + 1
end
sum = 0
si = []
count.each do |v|
si.push sum
sum = sum + v
end sc = Array.new(4) {0}
temp.each do |i|
ix = ((q[i].x - @x)/hs).to_i
iy = ((q[i].y - @y)/hs).to_i
id = ix + iy * 2
j = si[id] + sc[id]
index[j] = i
sc[id] = sc[id] + 1
end
@nodes.push Node.new(hs, @x, @y)
@nodes.push Node.new(hs, @x+hs, @y)
@nodes.push Node.new(hs, @x, @y+hs)
@nodes.push Node.new(hs, @x+hs, @y+hs)
4.times do |i|
@nodes[i].divide(si[i],count[i],index,q)
end
end
end
分割メソッドdivideに、配列の最初の位置s、粒子数len、粒子のインデックス配列index、そして粒子の座標データqが渡されている。その後、以下のような処理を行っている。
indexを破壊的にソートするため、必要な部分配列をtempにコピー- どの部分に何個粒子があるのか数える。その数は
count[4]に入る - そこから、ソートされた後にそれぞれの部分空間に属す粒子の「開始位置」がどこになるかを計算し、
si[4]に格納する。 indexに、ソート結果を(破壊的に)書き戻す。2
上記の処理により、粒子番号が空間インデックスによりソートされ、その開始位置と数がわかる。図解するとこんな感じ。

このうち、配列indexのsi[0]番目からcount[0]個の要素のソートを空間インデックス0番を担当する子ノードに依頼すれば良い。それをやっているのがこの部分。
@nodes.push Node.new(hs, @x, @y)
@nodes.push Node.new(hs, @x+hs, @y)
@nodes.push Node.new(hs, @x, @y+hs)
@nodes.push Node.new(hs, @x+hs, @y+hs)
4.times do |i|
@nodes[i].divide(si[i],count[i],index,q)
end
まとめ
Barnes-Hut treeの構築 (分布数えソート版)を作ってみた。insertion版だとシリアルに実行するしか無いが、この方式なら、各ノードにバラけたあとは同時に実行できるので、並列化とも相性が良いかもしれない?3
 A Robot’s Sigh
A Robot’s Sigh