制限ボルツマンマシンの基礎 ~コスト関数編~
はじめに
機械学習で用いられるボルツマンマシン、特に制限ボルツマンマシン(Restricted Boltzmann Machine, RBM)の解説その3です。その2の続きなので、そちらを見てから読んでください。
前回までのあらすじ
ぼっち飯のDaveは、いつも学食前のテラスでお弁当を食べていますが、同じクラスのAliceとBobが学食をよく利用していることに気づきます。しかし、AliceとBobは同時に現れることは少ないようです。AliceとBobは仲が悪いのでしょうか?
Daveは何日も二人を観測し、以下のようなデータを得ました。
そこでDaveは239日にわたって二人を観察し、AliceとBobが学食に来た日、来ていない日の統計を取りました。
| A | B | 日数 |
|---|---|---|
| x | x | 35 |
| x | o | 56 |
| o | x | 113 |
| o | o | 35 |
Daveはさらに、この二人が「名前は知っているくらいで、特にお互い好きでも嫌いでもない」という情報から、「学食になんらかの隠れ変数があり、その変数を通じて二人が間接的に相互作用している」というモデルを作ります。Daveはこれが、制限ボルツマンマシンという、人工ニューラルネットワークモデルの一種であることを知ります。前回、全てのパラメータを気合で手で決定しましたが、適切なコスト関数を定義できれば、他のニューラルネットワークモデルと同様に最適化アルゴリズムによりパラメータを決めることができるはずです。
しかし、そこでDaveは悩みます。他のニューラルネットのコスト関数はなんとなくわかる。でも制限ボルツマンマシンの学習のコスト関数とはなんだろう?そもそも制限ボルツマンマシンの学習とはどういうものだろう?
以下では、Daveの代わりにボルツマンマシンの学習について確認してみましょう。
コスト関数
学習とは、多数のパラメータを持つモデルが、望ましい振る舞いをするようにパラメータを調整することです。その際、適当なコスト関数(ロス関数)を定義し、そのコスト関数を最も小さくするようなパラメータを探す、最適化問題に落とすことがよく行われます。
例えばネコかイヌが写っている写真を見て、どちらが写っているか判定するAIを作りたいとしましょう。その場合、写真と正解ラベルのセットを大量に用意し、ニューラルネットワークに学習させ(学習フェーズ)、その後に学習に使っていない写真に対して正しく判定できたら学習がうまく行ったと判断できます(確認フェーズ)。このように「入力データ」と「正解」がセットで与えられてるようなパターンの機械学習を教師あり学習(supervised learning)と呼びます。教師あり学習は、正解が離散的な分類問題と、正解が連続的な回帰問題に分けることができます。写真を見て何が写っているかを判定するのが分類問題、人が写っている写真を見て年齢を推定するのが回帰問題です。
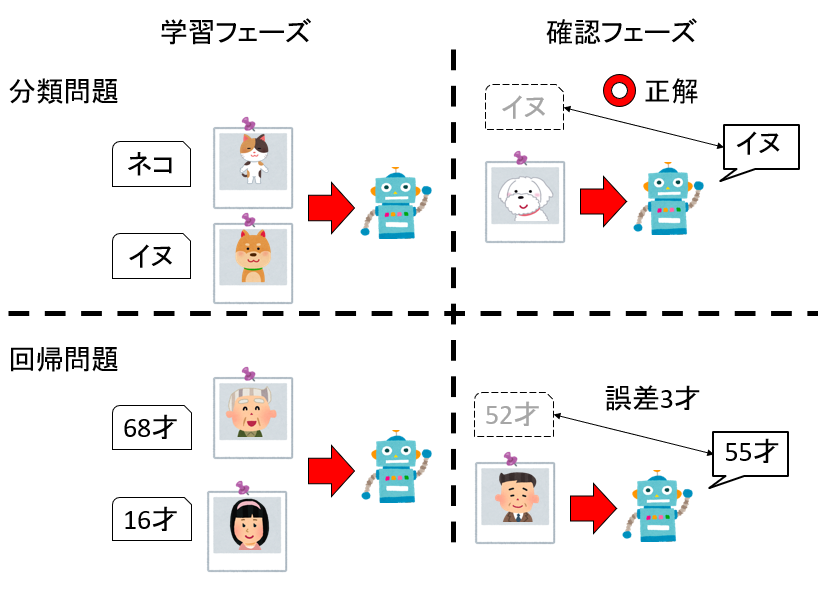
このような教師あり学習においてコスト関数の定義は簡単です。例えば分類問題なら誤答率をコスト関数にすれば、コスト関数を最適化することが誤答を減らすことにつながり、結果として正しい分類器を得ることができます。分類器では、多クラス交差エントロピー(categorical cross entropy)をコスト関数として採用することが多いです。 回帰問題でも、正解とモデルの予測値の誤差の二乗か絶対値の和をコスト関数とすれば、コスト関数を下げれば下げるほど正解に近い、良いモデルができたことになります。
一方、ボルツマンマシンの学習では、入力データは与えますが、正解データはありません。ボルツマンマシンは入力データの「癖」を覚える確率マシンであり、何らかの正解率を上げたり、誤差率を減らしたりするものではありません。ではボルツマンマシンは何を学習しているのでしょうか?
対数尤度関数
たくさんのデータを与えると、ボルツマンマシンはそのデータの癖を覚えます。先程のAliceとBobの例なら、Aliceだけ、Bobだけが学食にくる確率に比べて、AliceとBobが同時に学食に来る確率が低いことを学びます。
ボルツマンマシンは確率モデルなので、問い合わせるたびに何か確率的な出力をします。従って、実際におきる現象を予言できる確率を高くすることを目的としましょう。
起きる現象としては、AliceとBobがそれぞれ学食に来る、来ないの4通りです。この現象に以下のように通し番号(インデックス)をつけましょう。
| インデックス | A | B |
|---|---|---|
| 0 | x | x |
| 1 | x | o |
| 2 | o | x |
| 3 | o | o |
観測を始めてから、$t$日目の観測結果を$Y_t$とします。$Y_t$の値は$0,1,2,3$のいずれかです。
さて、ボルツマンマシンに$t$日目の観測結果を予想させたとして、その予想結果を$\hat{X}_t$としましょう。$\hat{X}_t$は確率変数で、その値も$0,1,2,3$のいずれかです。
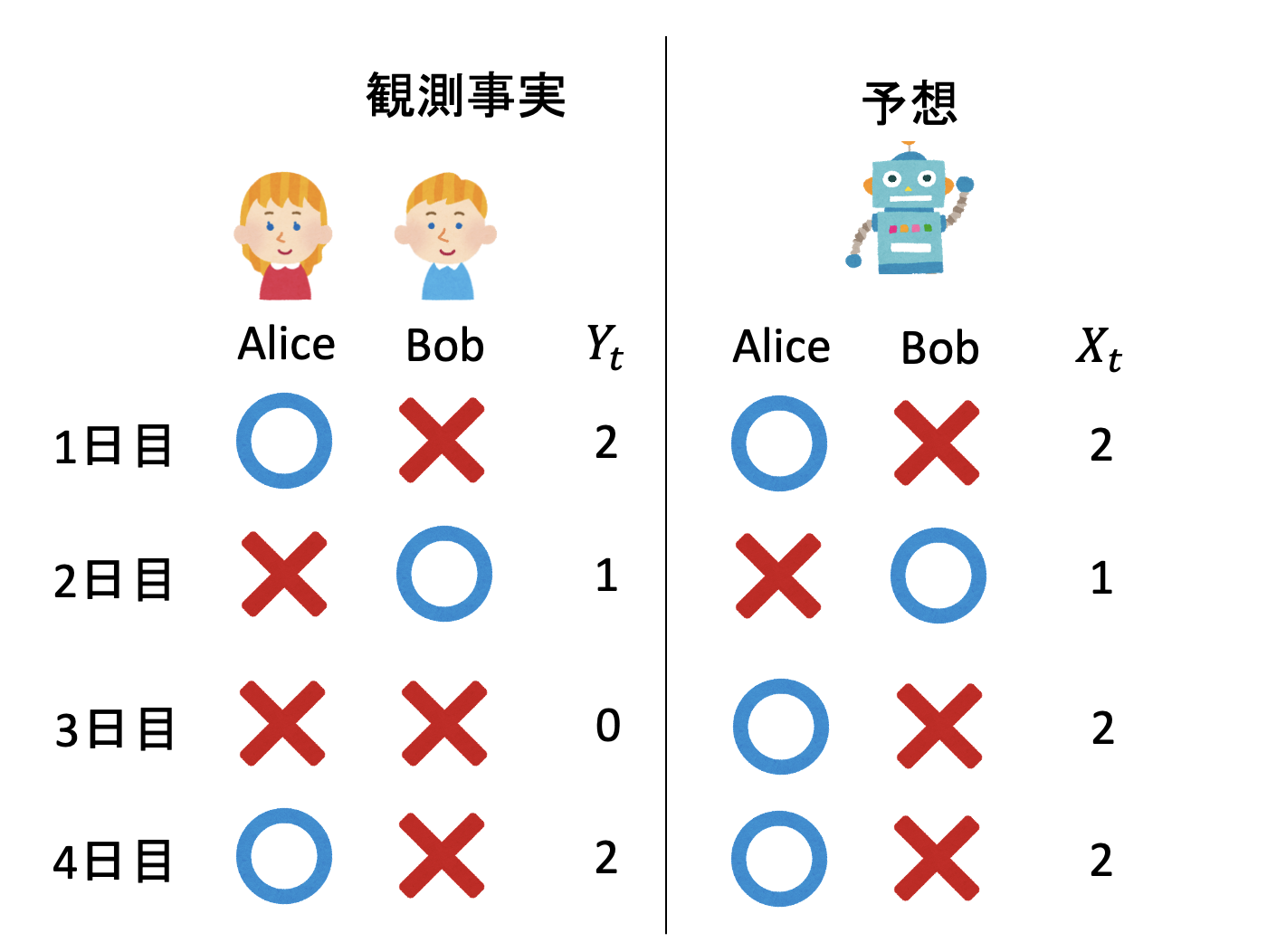
いま、$1$日目から$N$日目までの予想結果が完全に一致する確率$L$を考えましょう。
\[L = P(\hat{X}_1 = Y_1, \hat{X}_2 = Y_2, \cdots, \hat{X}_N = Y_N, )\]$\hat{X}_t$はボルツマンマシンのパラメータに依存する確率変数です。そこで、この$L$を尤度と考え、この値を最大化することを考えましょう。この値が大きいほど、ボルツマンマシンはうまく現象を説明できていることになります。
ここで、各観測結果が独立である、つまり、ある日にAliceとBobが学食に来たかどうかは次の日に影響しない(確率過程がマルコフ過程である)ことを仮定しましょう。すると、各事象が独立になるため、確率はそれぞれの事象の積にわかれます。
\[L = \prod_t^N P(\hat{X}_t = Y_t)\]これは積になっているので、対数をとると和になります。
\[\log L = \sum_t^N \log P(\hat{X}_t = Y_t)\]これは対数尤度関数に他なりません。対数は単調増加関数なので、対数をとっても最大化問題としては変わりません。
さらに、ボルツマンマシンマシンの出力$\hat{X}_t$は$t$に依存しないので、単に$\hat{X}$と書きましょう。
\[\log L = \sum_t^N \log P(\hat{X} = Y_t)\]これがボルツマンマシンの値に対して最大化すべき値です。
カルバック・ライブラー情報量
さて、Daveの統計によると、AliceとBobの学食への出現頻度は以下の表の通りでした。
| A | B | 日数 |
|---|---|---|
| x | x | 35 |
| x | o | 56 |
| o | x | 113 |
| o | o | 35 |
事象$i$が起きた確率を$q_i$としましょう。たとえば、観測日数239日のうち、二人とも学食に現れなかった日数は35日ですから、確率$q_0$は$35/239$です。 表にまとめると
| インデックス | A | B | 日数 | $q_i$ |
|---|---|---|---|---|
| 0 | x | x | 35 | $35/239$ |
| 1 | x | o | 56 | $56/239$ |
| 2 | o | x | 113 | $113/239$ |
| 3 | o | o | 35 | $35/239$ |
$N$日のうち、事象$i$がおきた回数は$N q_i$回あるので、和を$t$から$i$に取り直すことができます。
\[\log L = N \sum_i q_i \log P(\hat{X} = i)\]さて、ボルツマンマシンマシンの出力$\hat{X}$が、$i$に等しい確率$P(\hat{X}_t = i)$を$p_i$と書きましょう。具体的に書くとこんな感じです。
\[\begin{aligned} p_0 &\equiv P(\hat{X}_t = 0)\\ p_1 &\equiv P(\hat{X}_t = 1)\\ p_2 &\equiv P(\hat{X}_t = 2)\\ p_3 &\equiv P(\hat{X}_t = 3)\\ \end{aligned}\]この表記を用いると、対数尤度関数は以下のようになります。
\[\frac{1}{N}\log L = \sum_i q_i \log p_i\]両辺を$N$で割りました。
ここで、$q_i$は観測事実によって決まるので(ボルツマンマシンのパラメータにとって)定数です。したがって、$q_i \log q_i$も、それを$i$に関して和をとった$\sum_i q_i \log q_i$も定数です。両辺から引いてみましょう。
\[\begin{aligned} \frac{1}{N}\log L - \sum_i q_i \log q_i &= \sum_i q_i \log p_i - \sum_iq_i \log q_i\\ &=\sum_i (q_i \log p_i - q_i \log q_i) \\ &= \sum_i q_i \log \frac{p_i}{q_i} \\ &= - \sum_i q_i \log \frac{q_i}{p_i} \\ &= - D_\mathrm{KL} (\vec{q} | \vec{p}) \end{aligned}\]| 最後の$D_\mathrm{KL} (\vec{q} | \vec{p})$は、分布$\vec{q}$に対する分布$\vec{p}$のカルバック・ライブラー情報量(Kullback–Leibler divergence)です。 |
2つの分布$\vec{q},\vec{p}$が完全に一致している場合、つまり全ての$i$について$q_i = p_i$が成り立つ場合は、$\log q_i/p_i = 0$となるため、この量はゼロとなります。また、$\sum_i p_i = 1$であることから、この量は必ず非負の実数となります1。
以上から、カルバック・ライブラー情報量は、二つの分布の間の距離のような量であり、小さければ小さいほど、二つの分布が似ていることを意味します。
我々は左辺を最大化したかったのですから、それは右辺を最小化することになります。すなわち、モデルが現象をうまく説明している(対数尤度を最大化する)とは、現象の分布とモデルが生成する分布を似せる(2つの分布のカルバック・ライブラー情報量を最小化する)のと等価であることがわかりました。
まとめ
ボルツマンマシンの予測の精度を、「現象を完全に説明できる確率」として定義すると、モデルの対数尤度関数を最大化する問題に帰着すること、そしてそれは現象の分布と、モデルが生成する分布のカルバック・ライブラー情報量を最小化する問題と等価であることを見ました。
ボルツマンマシンは教師なし学習であるため、教師あり学習に比べて「何を最適化しているのか」がわかりにくい傾向にあります。しかし、対数尤度関数を最大化する問題であると思うと、例えば表が出る確率$p$が1/2でない不公平なコインがあったとして、多数回コインを投げた結果(観測事実)から、$p$を推定する問題と同じであることがわかるでしょう。ボルツマンマシンにおける学習とは、要するにパラメータの最尤推定に過ぎません。
しかし、実際にパラメータの最尤推定をしようとすると、ボルツマンマシンのスピンの数に対して 指数関数的に計算が大変になり、それがボルツマンマシンの学習のネックとなりました。この問題を解決したのが制限ボルツマンマシンと、Contrastive Divergence法です。この、パラメータで真面目に微分してみて、計算が大変になるあたりまでを次回の「制限ボルツマンマシンの基礎 〜微分編〜」にまとめる予定です。
-
証明にはJensenの不等式を使いますが、ここでは省略します。詳細は「カルバック・ライブラー情報量 非負性」などで調べてください。 ↩
 A Robot’s Sigh
A Robot’s Sigh