[Up] [Repository]

• 正準変換
• 母関数

本章で学ぶこと

ニュートンの運動方程式からラグランジュ形式の運動方程式に移ったのは、点変換という任意の座標変換について運動方程式の形が共変となるからであった。さらに、ラグランジアンをルジャンドル変換することによってハミルトニアンを作ると、座標と運動量が混ざるような、より広い変数変換を許容することになる。この、ハミルトンの運動方程式を共変に保つような変数変換を正準変換と呼ぶ。以下では正準変換を様々な角度から考察する。

正準変換

オイラー・ラグランジュ方程式は一般化座標について任意の変換(点変換)を行っても方程式の形が変わらなかった。ハミルトンの運動方程式は、点変換のみならず、\(p\) と\(q\) を混ぜるような、より広い範囲の変換について共変となる。しかし、その変換は完全に任意というわけではなく、その変換規則には制限がつく。いま、変数変換 \((q,p) \rightarrow (Q, P)\) により、ハミルトンの運動方程式が共変に保たれるためには、どのような条件が必要であるかを調べてみよう。

我々が調べたいことは、元の変数 \((q,p)\)がハミルトンの運動方程式

\[ \begin{aligned} \dot{q} &= \frac{\partial H}{\partial p} \\ \dot{p} &= -\frac{\partial H}{\partial q} \\ \end{aligned} \]

を満たす時、新たな変数 \((Q,P)\) が同じ形の運動方程式

\[ \begin{aligned} \dot{Q} &= \frac{\partial H}{\partial P} \\ \dot{P} &= -\frac{\partial H}{\partial Q} \\ \end{aligned} \]

を満たすための条件、すなわちハミルトンの運動方程式が変数変換に対して共変となる条件である。まず、ハミルトニアンを\((Q,P)\)で書いておく。そして\((Q,P)\)を\((q,p)\)の関数だと思って偏微分しよう。

\[ \begin{aligned} \dot{q} &= \frac{\partial H}{\partial p} \\ &= \frac{\partial H(Q(q,p),P(q,p))}{\partial p} \\ &= \frac{\partial H}{\partial Q}\frac{\partial Q}{\partial p} * \frac{\partial H}{\partial P}\frac{\partial P}{\partial p} \end{aligned} \]

同様に、

\[ \begin{aligned} \dot{p} &= -\frac{\partial H}{\partial q} \\ &= -\frac{\partial H}{\partial Q}\frac{\partial Q}{\partial q} * \frac{\partial H}{\partial P}\frac{\partial P}{\partial q} \end{aligned} \]

次に、新たな変数\(Q\)の時間微分を考えよう。計算がごちゃごちゃしがちなので、丁寧に計算する。

\[ \begin{aligned} \dot{Q} &= \frac{d}{dt} Q(q,p) \\ &= \frac{\partial Q}{\partial q}\dot{q} +\frac{\partial Q}{\partial p} \dot{p} \\ &= \frac{\partial Q}{\partial q} \underbrace{\left( \frac{\partial H}{\partial Q}\frac{\partial Q}{\partial p} * \frac{\partial H}{\partial P}\frac{\partial P}{\partial p} \right)}_{\dot{q}} \\ &- \frac{\partial Q}{\partial p} \underbrace{\left( \frac{\partial H}{\partial Q}\frac{\partial Q}{\partial q} + \frac{\partial H}{\partial P}\frac{\partial P}{\partial q} \right)}_{\dot{p}}\\ &=\cancel{\frac{\partial Q}{\partial q} \frac{\partial H}{\partial Q}\frac{\partial Q}{\partial p}} + \frac{\partial Q}{\partial q}\frac{\partial H}{\partial P}\frac{\partial P}{\partial p} \\ &- \cancel{\frac{\partial Q}{\partial p}\frac{\partial H}{\partial Q}\frac{\partial Q}{\partial q}} - \frac{\partial Q}{\partial p}\frac{\partial H}{\partial P}\frac{\partial P}{\partial q} \\ &= \frac{\partial H}{\partial P}\left(\frac{\partial Q}{\partial q}\frac{\partial P}{\partial p} - \frac{\partial Q}{\partial p}\frac{\partial P}{\partial q} \right) \end{aligned} \]

詳細は省略するが\(\dot{P}\)も全く同様に計算できる。合わせて書くと、

\[ \begin{aligned} \dot{Q} &=\frac{\partial H}{\partial P}\left(\frac{\partial Q}{\partial q}\frac{\partial P}{\partial p} - \frac{\partial Q}{\partial p}\frac{\partial P}{\partial q} \right) \\ \dot{P} &= -\frac{\partial H}{\partial Q}\left(\frac{\partial Q}{\partial q}\frac{\partial P}{\partial p} - \frac{\partial Q}{\partial p}\frac{\partial P}{\partial q} \right) \end{aligned} \]

したがって、変数変換\((p,q) \rightarrow (P,Q)\)により、ハミルトンの運動方程式が共変であるためには、この変数変換が以下の条件を満たす必要がある。

\[ \frac{\partial Q}{\partial q}\frac{\partial P}{\partial p} - \frac{\partial Q}{\partial p}\frac{\partial P}{\partial q} = 1 \]

この条件を満たす変数変換を 正準変換(canonical transform) と呼ぶ。先程の条件は、行列式の形にまとめることができる。

\[ \begin{vmatrix} \partial_q Q & \partial_p Q \\ \partial_q P & \partial_p P \end{vmatrix} =1 \]

これは、変換\((p,q) \rightarrow (P,Q)\)のヤコビアンに他ならない。すなわち、正準変換とは、変換のヤコビアンが1となるような変換のことである。逆に言えば、ヤコビアンが1でありさえすれば、どのような変換を行おうとハミルトンの運動方程式は共変である。点変換しか許容しなかったラグランジアンに比べて、変換の幅が広がったことがわかる。

いくつか正準変換の例を挙げよう。まずは座標を\(Q=Q(q)\)と変換する点変換を考えよう。もともとの系がラグランジアン\(L(q, \dot{q})\)に従っていたとすると、運動量の定義から

\[ p = \frac{\partial L}{\partial \dot{q}} \]

である。ここで、\(Q=Q(q)\)を\(Q\)について解いて\(q=q(Q)\)とする。\(\dot{q}\)を計算すると

\[ \begin{aligned} \dot{q} &= \frac{d q(Q)}{dt} \\ &= \frac{dq}{dQ}\dot{Q} \end{aligned} \]

\(dq/dQ\)は\(Q\)の関数であるから、\(\dot{q}\)は\(Q\)と\(\dot{Q}\)の両方に依存している。したがって、\(\dot{q}(Q,\dot{Q})\)と書ける。以上から、もとのラグランジアンを\((Q,\dot{Q})\)の関数として表現すると、\(L(q(Q), \dot{q}(Q,\dot{Q})\)と書ける。

新たな運動量\(P\)は

\[ \begin{aligned} P &= \frac{\partial}{\partial \dot{Q}} L(q(Q), \dot{q}(Q,\dot{Q}) \\ &= \underbrace{\frac{\partial L}{\partial \dot{q}}}_{=p} \underbrace{\frac{d \dot{q}}{d \dot{Q}}}_{dq/dQ} \\ &= \frac{p}{Q'} \end{aligned} \]

と書ける。

\(P\)と\(Q\)の \((q,p)\)依存性がわかったのでヤコビアンを計算してみよう。

\[ \begin{vmatrix} \partial_q Q & \partial_p Q \\ \partial_q P & \partial_p P \end{vmatrix} = \begin{vmatrix} Q' & 0 \\ \partial_q P & 1/Q' \end{vmatrix} =1 \]

すなわち、点変換は正準変換である。

次に以下の変換を考えよう。

\[ \begin{aligned} Q &= p \\ P &= -q \end{aligned} \]

これは座標と運動量を入れ替えて、片方に負符号をつけたものだ。ヤコビアンは簡単に計算できて、

\[ \begin{vmatrix} \partial_q Q & \partial_p Q \\ \partial_q P & \partial_p P \end{vmatrix} = \begin{vmatrix} 0 & 1 \\ -1 & 0 \end{vmatrix} =1 \]

となるから、これは正準変換である。

もともと

\[ \begin{aligned} \dot{q} &= \frac{\partial H}{\partial p} \\ \dot{p} &= -\frac{\partial H}{\partial q} \end{aligned} \]

が成り立っている時、\(\dot{Q}, \dot{P}\)を計算すると、

\[ \begin{aligned} \dot{Q} &= \dot{p} = -\frac{\partial H}{\partial q} = \frac{\partial H}{\partial P} \\ \dot{P} &= -\dot{q} = - \frac{\partial H}{\partial p} =- \frac{\partial H}{\partial Q} \end{aligned} \]

と、新たな変数 \((Q,P)\)も、ハミルトンの運動方程式に従うことがわかる。このように、正準変換は座標と運動量が入れ替わるような変換を許容する。

より一般に、座標と運動量を混ぜるような変換を考えよう。

\[ \begin{aligned} Q &= \sqrt{2q} \cos p \\ P &= \sqrt{2q} \sin p \end{aligned} \]

ヤコビアンを計算すると、

\[ \begin{aligned} \begin{vmatrix} \partial_q Q & \partial_p Q \\ \partial_q P & \partial_p P \end{vmatrix} &= \begin{vmatrix} \displaystyle\frac{\cos p}{\sqrt{2q}} & - \sqrt{2q} \sin p \\ \displaystyle\frac{\sin p}{\sqrt{2q}} & \sqrt{2q} \cos p \end{vmatrix}\\ & = \cos^2 p + \sin^2 p\\ &=1 \end{aligned} \]

すなわち、先程の変換は正準変換である。

母関数

変数変換\((q,p) \rightarrow (Q, P)\)が正準変換であるためには、そのヤコビアンが\(1\)である必要があった。ある変換が正準変換であるかどうかを確認するためには、1自由度系なら2行2列の行列の行列式、\(N\)自由度系なら\(2N\)行\(2N\)列の行列のヤコビアンを計算する必要がある。もともと、\(2N\)本の運動方程式をただ一つのスカラー関数から表現できるというのがラグランジアンやハミルトニアンのメリットであった。そこで、\(2N\)個の変数から\(2N\)個の変数への変数変換を、一つのスカラー関数から生み出したい。そのような関数がここで説明する母関数である。

ある変換\((q,p) \rightarrow (Q, P)\)が正準変換であるとは、それぞれが正準方程式を満たす、すなわちこの変換が正準方程式を共変に保つことを指すのであった。一方、正準共役な変数\((q,p)\)が満たす正準方程式は

\[ \begin{aligned} \dot{q} &= \frac{\partial H}{\partial p} \\ \dot{p} &= -\frac{\partial H}{\partial q} \end{aligned} \]

であるが、これはもともと作用積分

\[ I = \int_{t_1}^{t_2} (p\dot{q} - H(q,p))dt \]

の変分から得られたものであった。同様に変換後の変数\((Q,P)\)が正準方程式を満たすならば、やはり作用積分

\[ I = \int_{t_1}^{t_2} (P\dot{Q} - H(Q,P))dt \]

の変分\(\delta I = 0\)から得られる。したがって、正準方程式と作用積分は等価である。\(N\) 自由度系の正準方程式では\(2N\) 自由度の変数の間の関係を調べる必要があったが、変分原理まで戻ればスカラー関数一つについての等価性を調べれば良い。作用積分の被積分関数はスカラー関数であるから、正準変換\((q,p) \rightarrow (Q,P)\)も、変分原理まで戻ればスカラー関数だけで考えられるはずである。すなわち、ハミルトニアンになんらかの関数\(F\)を加えた\(H+F\)について作用積分

\[ I = \int_{t_1}^{t_2} (p\dot{q} - H(q,p) + F(q,p))dt \]

を考え、これを改めて新たな変数\((Q,P)\)で

\[ I = \int_{t_1}^{t_2} (P\dot{Q} - H(Q,P))dt \]

と書き直せたとする。後者については変分原理から\((Q,P)\)に関する正準方程式を導くため、前者として正準方程式を変えないような\(F\)を探すことができれば、この変換は正準変換を導くことになる。

まず、自明な例として、ハミルトニアンに定数を加えても結果は変わらない。もう少し非自明な例として、作用積分に\(q\dot{q}\)という量を加えたものに対して変分を考えてみよう。

\[ \begin{aligned} \delta(p\dot{q} - H + q \dot{q}) &= \delta(p\dot{q} - H ) + \delta(q\dot{q}) \\ &= \delta(p\dot{q} - H) + \dot{q}\delta q + q \delta \dot{q} \\ &= \delta(p\dot{q} - H) + \underbrace{\dot{q}\delta q - \dot{q} \delta q}_{=0} \end{aligned} \]

と、部分積分により付け加えた項がゼロになるため、項をつけわえる前と同じ正準方程式が得られる。すなわち、ハミルトニアン\(H\)に対して\(H \rightarrow H - q\dot{q}\)という変換は正準方程式を共変に保つため、正準変換を導く。

全く同様にして、\(q\)に関する任意の関数\(W(q)\)について、作用積分にその時間微分\(-dW/dt\)を加えても正準方程式を変えないことがわかる(あとのために負符号をつけておく)。実際に

\[ \begin{aligned} \delta\left(p\dot{q} - H - \frac{dW}{dt}\right) &= \delta (p\dot{q} - H - W'(q) \dot{q})\\ &= \delta(p\dot{q} - H) - \delta (W'(q) \dot{q}) \\ &= \delta(p\dot{q} - H) - W''(q) \dot{q} \delta q - W'(q) \delta \dot{q} \\ &= \delta(p\dot{q} - H) - \underbrace{W''(q) \dot{q} \delta q + W''(q) \dot{q}\delta q}_{=0} \\ \end{aligned} \]

となり、部分積分で消えてしまう。\(W\)が\(p\)のみの関数の場合も同様である。したがって、ハミルトニアンに加える項として\(F = dW/dt\)を考えれば正準変換を導けそうである。ただし、\(W\)が\(q,p\)のどちらにも依存する場合、\(W\)が正準変換を導くには条件がつく。

いま、\((q,p)\)で記述されたハミルトニアン\(H(q,p)\)に、任意の関数\(W(q,p)\)を考え、その時間微分\(F=-dW/dt\)を加えたものの変分を考えよう。

\[ \delta\left(p\dot{q} - H - \frac{dW}{dt}\right) = \delta (p\dot{q} - H) - \delta \left(\frac{dW}{dt} \right) \]

であるから、\(\delta \dot{W} = 0\)であれば元の正準方程式を導く。計算してみると、

\[ \begin{aligned} \delta \dot{W} &= \delta \left(\frac{\partial W}{\partial q}\dot{q} + \frac{\partial W}{\partial p}\dot{p} \right) \\ &= \underbrace{\delta \left(\frac{\partial W}{\partial q}\right)\dot{q} + \frac{\partial W}{\partial q} \delta \dot{q}}_{\bigstar} + \delta \left(\frac{\partial W}{\partial p}\right)\dot{p} + \frac{\partial W}{\partial p} \delta \dot{p} \\ \end{aligned} \]

右辺の第一項、第二項を計算すると、

\[ \begin{aligned} \bigstar &= \delta \left(\frac{\partial W}{\partial q}\right)\dot{q} - \frac{d}{dt}\left(\frac{\partial W}{\partial q}\right) \delta q \\ &= \cancel{\frac{\partial^2 W}{\partial q^2} \dot{q} \delta q} + \frac{\partial^2 W}{\partial q \partial p} \dot{q} \delta p + \cancel{\frac{\partial^2 W}{\partial q^2} \dot{q} \delta q} + \frac{\partial^2 W}{\partial q \partial p} \dot{p} \delta q \end{aligned} \]

したがって、\(W(q,p)\)が

\[ \frac{\partial^2 W}{\partial q \partial p} = 0 \]

という条件を満たせば、この項は消える。残りの\(\dot{p}\)に関する項も同様である。以上から、2つの引数両方に関する偏微分がゼロであるような関数\(W\)の時間微分をハミルトニアンに加えても正準方程式を変えない、すなわちこの関数が以下の正準変換を導くことがわかった。

\[ p\dot{q} - H(q,p) - \frac{dW}{dt} = P \dot{Q} - H(Q,P) \]

ここから変数の間の変換公式を得るため、\(dW/dt\)について整理しよう。また、後のために時間微分をニュートン表記からライプニッツ表記で書き直す。ハミルトニアン\(H\)は(時間非依存であれば)変数を書き直しただけで値は変わらないため、両辺でキャンセルする。

\[ \frac{dW}{dt} = p\frac{dq}{dt} - P \frac{dQ}{dt} \]

両辺に形式的に\(dt\)をかけると

\[ dW = p dq - P dQ \]

これは、関数\(W\)が自由変数を\(q, Q\)とみなした時の全微分の表式となっている。全微分の定義から

\[ dW(q, Q) = \frac{\partial W}{\partial q} dq + \frac{\partial W}{\partial Q}dQ \]

であるから、両者を比較すると、

\[ \begin{aligned} p &= \frac{\partial W}{\partial q} \\ P &= - \frac{\partial W}{\partial Q} \end{aligned} \]

を得る。すなわち、先程の条件を満たす任意の関数\(W(q,Q)\)を考えると、 \((q,Q)\)から新たな変数の組\((p(q,Q),P(q,Q))\)が得られる。これを\((P,Q)\)について解き直せば

\[ \begin{aligned} Q &= Q(q,p) \\ P &= P(q,p) \end{aligned} \]

という正準変換\((q,p) \rightarrow (Q,P)\)を作ることができる。このように、\(W\)は正準変換を生み出す関数となっているため、 母関数(generating function) と呼ぶ。

母関数は、変換前後の変数をそれぞれ含んでなければならない。先程の正準変換の母関数\(W(q,Q)\)は、新旧の一般化座標を引数としていた。これをType 1と呼び、慣習的に\(W_1\)と表す。ここからルジャンドル変換により自由変数を取り直そう。

\[ W_2 = W_1 + PQ \]

により新たな関数\(W_2\)を考えると、

\[ \begin{aligned} d W_2 &= d W_1 + QdP + PdQ \\ &= pdq - \cancel{PdQ} + QdP + \cancel{PdQ}\\ &= pdq + QdP \end{aligned} \]

ここから、\(W_2\)の自由変数は\(q, P\)であり、変換則は

\[ \begin{aligned} p &= \frac{\partial W_2}{\partial q}\\ Q &= \frac{\partial W_2}{\partial P}\\ \end{aligned} \]

で与えられる。

同様に、\(W_3 = W_1 - pq\)とすることで、

\[ d W_3 = -qdp - PdQ \]

となるため、変換則は

\[ \begin{aligned} q &= -\frac{\partial W_3}{\partial p}\\ P &= -\frac{\partial W_3}{\partial Q}\\ \end{aligned} \]

さらに、\(W_4 = W_3+PQ\)とすることで、

\[ d W_4 = -qdp + QdP \]

から、変換則は

\[ \begin{aligned} q &= -\frac{\partial W_4}{\partial p}\\ Q &= \frac{\partial W_4}{\partial P}\\ \end{aligned} \]

となる。以上をまとめると以下のような図となる。

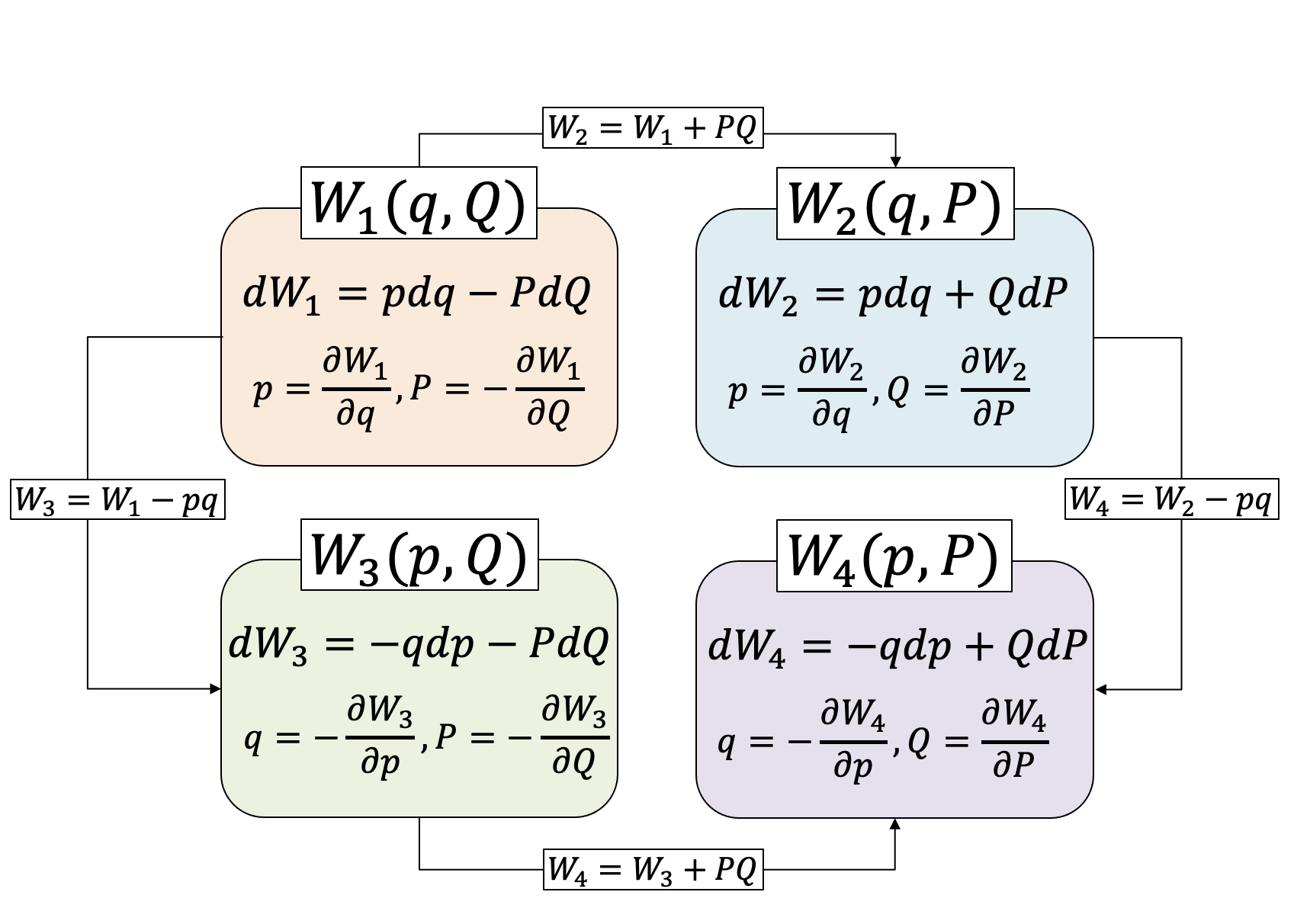
図で見ると複雑に感じるかもしれないが、以下のルールを知ればさほど難しくはない。

• 母関数は新旧の変数を一つずつ含む
• その組み合わせは\(W_1(q,Q), W_2(q,P), W_3(p, Q), W_4(p, P)\)の四種類ある
• 変換則は母関数を自由変数で偏微分することで、正準共役な変数が得られる
• 偏微分した際の符号は、全微分からわかる
• 母関数同士はルジャンドル変換で繋がっている

これらはの母関数は、以下の条件さえ満たせば任意に選ぶことができる。

\[ \begin{aligned} \frac{\partial^2 W_1}{\partial q \partial Q} &= 0 \\ \frac{\partial^2 W_2}{\partial q \partial P} &= 0 \\ \frac{\partial^2 W_3}{\partial p \partial Q} &= 0 \\ \frac{\partial^2 W_4}{\partial p \partial P} &= 0 \end{aligned} \]

逆に言えば、この母関数から作られる変換は正準変換となる。

母関数による正準変換について、いくつか簡単な例を挙げておこう。

まず、\(W_2(q,P)=qP\)を採用すると

\[ \begin{aligned} p &= \frac{\partial W_2}{\partial q} = P\\ Q &= \frac{\partial W_2}{\partial P} = q\\ \end{aligned} \]

となり、これは恒等変換を表す。

\(W_1(q, Q) = qQ\)を採用すると

\[ \begin{aligned} p &= \frac{\partial W_1}{\partial q} = Q\\ P &= -\frac{\partial W_1}{\partial Q} = -q \end{aligned} \]

となるので、改めて\((Q,P)\)を\((q,p)\)の関数として書き直すと、

\[ \begin{aligned} Q &= p \\ P &= -q \end{aligned} \]

つまり、座標と運動量と入れ替えて負符号をつける変換になっている。同様に、\(W_1(q,Q) = -qQ\)を採用すれば、

\[ \begin{aligned} Q &= -p \\ P &= q \end{aligned} \]

と、符号が逆転する。このように正準変換においては座標と運動量を自由に入れ替えることができる。

まとめ

ニュートンの運動方程式からラグランジュ形式の力学に移ったのは、もともと変数変換に強いから、という目的があった。ハミルトン形式の力学に移ると、ラグランジュ形式の力学よりもさらに広い形の変数変換を許容するようになった。この変数変換を正準変換と呼ぶ。しかし、これは単に問題を解くために便利なように変数変換をするという目的を超え、そもそも時間発展とは正準変換である、ということが示された。さらに、系に連続的な変化を及ぼす操作を行った場合、その操作でハミルトニアンが変化しない(変化が高次となる)場合、その操作に対応する保存量が存在することがわかった(ネーターのの定理)。この定理は非常に一般的かつ強力であり、例えば操作として時間変化を選ぶとエネルギー保存則が、空間並進を選ぶと運動量保存則が、回転を選ぶと角運動量保存則が得られる。すなわち、ネーターの定理は、系が持つ連続対称性と保存量の関係を極めて一般的に結びつけている。位相空間の章で、時間発展がまるで回転のように見えた。この章でもやはり、時間発展、空間並進、回転が全て同じように見えることは驚きである。