[Up] [Repository]

本章で学ぶこと

運動エネルギーを\(K\)、ポテンシャルエネルギーを\(U\)とすると、ラグランジアン\(L\)は\(L=K-U\)で与えられる。ここで、なぜ全エネルギー\(K+U\)ではなく、\(K-U\)なのか疑問に思う人も多いだろう。簡単にいえば「部分積分により負符号が出るから」なのだが、その物理的な意義は奥が深く、すぐに理解することは難しいかもしれない。以下では仮想仕事の原理と比較しながらラグランジアンの導出を行うことで、少なくとも数式上ではどのように\(K-U\)が出てくるかを理解する。また、多自由度系の運動方程式がただ一つのラグランジアンから導出されることを見る。

ラグランジアン

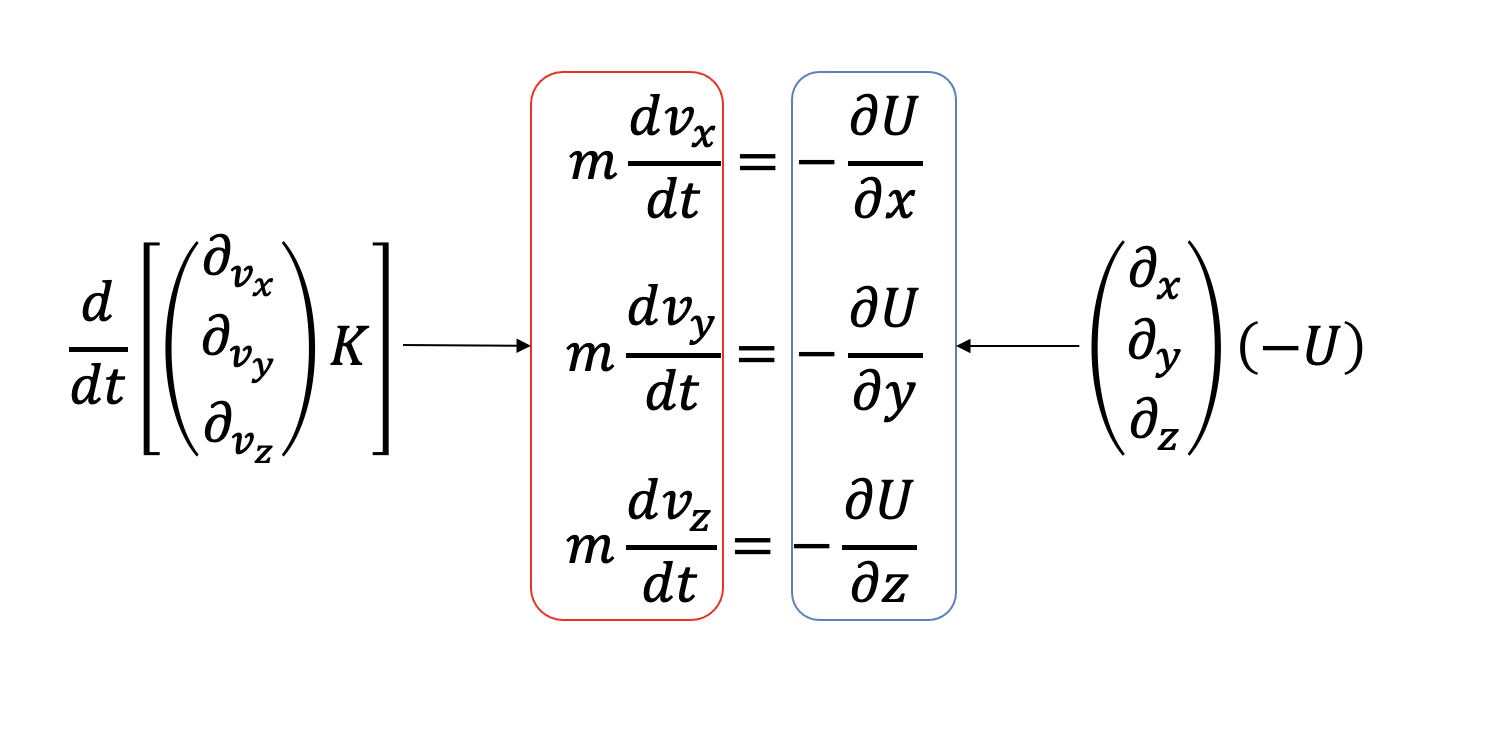
まず、ラグランジアンを発見法的に導出しておこう。3次元空間の場所\((x,y,z)\)に、運動がポテンシャル\(U(x,y,z)\)に支配されて運動する質点があるとする。この質点の質量を\(m\)とすると、運動方程式は

\[ \begin{aligned} m \dot{v_x} &= -\frac{\partial U}{\partial x}\\ m \dot{v_y} &= -\frac{\partial U}{\partial y}\\ m \dot{v_z} &= -\frac{\partial U}{\partial z}\\ \end{aligned} \]

という形に書ける。ここで、運動方程式の右辺が全てポテンシャルエネルギーの位置による偏微分になっていることに注目する。左辺も同様にポテンシャルを用意して、自由度で偏微分する形にすると運動方程式がきれいに書けそうである。運動において全エネルギーが保存しており、全エネルギーとは運動エネルギーと位置エネルギーの和であり、右辺に位置エネルギーが来ているなら、左辺には運動エネルギーが来るのが自然であろう。そこで、以下のような運動エネルギーを考える。

\[ K(v_x,v_y,v_z) = \frac{1}{2}m(v_x^2+v_y^2+v_z^2) \]

ポテンシャルエネルギーと同様に、自由度で偏微分してみよう。

\[ \frac{\partial K}{\partial v_x} = m v_x \]

運動方程式と見比べると、両辺を時間微分したくなる

\[ \frac{d}{dt}\left(\frac{\partial K}{\partial v_x}\right) = m \dot{v_x} \]

これは運動方程式の左辺である。以上から、運動方程式を以下のようにまとめることができた。

\[ \frac{d}{dt}\left(\frac{\partial K}{\partial v_x}\right) = -\frac{\partial U}{\partial x} \]

ポテンシャルエネルギーが運動方程式の右辺を作っており、運動エネルギーが左辺を作っていることがわかる。

\(v_x = \dot{x}\)と書くと、

\[ \frac{d}{dt}\left(\frac{\partial K}{\partial \dot{x}}\right) = -\frac{\partial U}{\partial x} \]

と、左右が同じ自由度\(x\)に由来するものであることが強調される。

さて、どうせ偏微分すると結果は同じであるから、\(K\)と\(U\)をまとめてしまおう。

\[ L(x,y,z,\dot{x},\dot{y},\dot{z}) = K(\dot{x},\dot{y},\dot{z}) - U(x,y,z) \]

により運動全体のポテンシャル\(L\)を定義すると、運動方程式の\(x\)成分は

\[ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) = \frac{\partial L}{\partial x} \]

と書ける。\(y\)、\(z\)成分も全く同様に書けるため、\((x,y,z)\)を\(x^1, x^2, x^3\)と記述すると、

\[ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}^i}\right) = \frac{\partial L}{\partial x^i} \]

と、3本の運動方程式が、ただ一つのスカラー関数でまとめて記述できるようになる。この関数\(L\)を ラグランジアン (Lagrangian) と呼ぶ。ここで、\(L = K - U\)と、運動エネルギーとポテンシャルエネルギーの差で表現した。なぜ和ではなく差なのかを理解するのが本章の目的である。

ラグランジアンを用いることのメリットは2つある。一つは、ラグランジアン一つだけで全ての自由度に関する運動方程式が記述できることである。今回は3自由度系を用いたが、質点が複数あるような超多自由度系であっても、適切なラグランジアンさえ選ぶことができれば、全ての自由度に関する運動方程式を得ることができる。すなわち、運動の全ての性質はラグランジアンが担うため、例えば保存則のような性質も全てラグランジアンに内在するはずであり、それらの性質を調べる際に見通しが良くなる。

もう一つのメリットは、運動をラグランジアンで記述すると、変数変換に強くなることである。もともと、運動方程式の右辺はポテンシャルエネルギーというスカラー関数で表現できていた。スカラー関数は変数変換に強く、異なる座標で表現しても、その座標で微分すれば、その方向の力を得ることができる。今回、運動エネルギーも「ポテンシャル」だと思って、運動方程式の左辺を記述した。従って、こちらも座標変換がやりやすくなることが予想される。ラグランジアンは、運動エネルギー、ポテンシャルエネルギーを合わせた、運動全体を記述するポテンシャルであることから、運動ポテンシャルと呼ばれることもある。スカラー関数により運動を記述していることから、本質的にベクトルに関する微分方程式であるニュートンの運動方程式よりも座標変換に強くなる。この事実は、後に点変換に対する共変性として示される。

ダランベールの原理

さて、発見法的に導出したラグランジアンを、もう少し理論的に導出しよう。仮想仕事の原理は、力が釣り合っており物体が静止している場合、すなわち静力学に適用する原理であった。これを動力学に応用することでラグランジアンが得られる。そのため、仮想仕事の原理の動力学版であるダランベールの原理について述べる。

ニュートンの運動方程式から始めよう。簡単のため、一次元空間の運動を考える。

\[ m \dot{v} = F \]

仮想仕事の原理では物体は静止していたために左辺はゼロであったが、今回は動いている場合を扱うのでゼロではない。さて、この運動方程式の左辺を右辺に移項しよう。

\[ 0 = - m \dot{v} + F \]

ここで、慣性項\(m v/dt\)を力とみなすと、式の上では力が釣り合っているかのように見える。これをダランベールの原理(d’Alembert’s principle) と呼ぶ。見かけ上、力が釣り合っているのであるから、静力学における仮想仕事の原理が適用できそうである。もし、\((x, v)\)が運動方程式を満たさなければ、上記は\(0\)からずれる。そこで、右辺を仮想的な力であるとみなし、\(F_D\)とおく。

\[ F_D = - m \dot{v} + F \]

そして、力\(F_D\)が働いている状態で、拘束条件を破らない仮想変位 \(\delta x\) だけ動いた時の仮想仕事を考える。

\[ W = F_D \delta x \]

もし、もともとの軌道\((x,v)\)が運動方程式を満たしている場合は\(F_D=0\)であったのだから、この力のする仮想仕事はゼロである。

\[ W = (- m \dot{v} + F) \delta x = 0 \]

これもダランベールの原理と呼ぶ。すなわちダランベールの原理とは、加速度がゼロでない時に、慣性項を移項することで、あたかも力であるように解釈し、その上で仮想仕事の原理を適用しようとするものである。ただし、速度の項があるため、静力学の場合は「力が釣り合っている時」だったのに対し、動力学の場合は「速度と位置が運動方程式の解である時」という条件に変わっていることに注意。

力が保存力である場合、

\[ F(x) = -U'(x) \]

であるから、

\[ W = - m \dot{v} \delta x -U(x) \delta x = 0 \]

となる。

さて、静力学における仮想仕事の原理では、釣り合いの位置\(x\)からの仮想的な変位\(x \rightarrow x + \delta x\)を考えた。動力学では、運動方程式を満たすような解\(x(t)\)から、少しだけずれたような軌道\(x(t) + \delta x(t)\)での運動を考える。すなわち、時間依存するような仮想変位\(\delta x(t)\)を考える。この時、ポテンシャルの変化は

\[ \begin{aligned} \delta U &\equiv U(x+\delta x) - U(x) \\ &= U'(x) \delta x +O(\delta x^2)\\ \end{aligned} \]

で与えられる。これを用いると、最終的にダランベールの原理は以下のように書ける。

\[ W = - m \dot{v}\delta x -\delta U = 0 \]

したがって、

\[ \delta U = - m \dot{v}\delta x \]

である。

左辺の\(\delta U\)とは、位置が\(x\)から\(x + \delta x\)に移動した時のポテンシャルエネルギーの変化分である。右辺は、いかにも運動エネルギーの変化分を表しているように見える。そこで、運動方程式の解から軌道が少しずれた時の、運動エネルギーの変化分を考えよう。運動エネルギーを速度\(v\)の関数

\[ K(v) = \frac{1}{2}mv^2 \]

とする。いま、運動方程式の解として\(x(t)\)が与えられたとしよう。すると、速度の時間依存性は\(v = \dot{x}\)で与えられる。この運動方程式の解から、少しだけずれた軌道\(X(t) = x(t) + \delta x(t)\)を考える。新しい軌道における速度を\(V(t) = v(t) + \delta v(t)\)とすると、\(\delta x\)と\(\delta v\)は

\[ \frac{d}{dt}\delta v = \delta x \]

を満たす。さて、新しい軌道ともとの軌道での運動エネルギーの変化\(\delta K\)は

\[ \begin{aligned} \delta K &\equiv K(v+\delta v) - K(v) \\ &=K'(v) \delta v \\ &= mv \delta v \\ &= mv \frac{d}{dt} \delta x \end{aligned} \]

先ほど得られたダランベールの原理

\[ \delta U = - m \dot{v} \delta x \]

と比較すると、部分積分したら\(\delta K\)になることがわかるであろう。これによりラグランジアンが導入される。

ハミルトンの原理とラグランジアン

時刻\(t_1\)から時刻\(t_2\)まで、運動方程式の解として、軌道\(x(t)\)が得られたとしよう。すると、時刻\(t\)での速度\(v(t)\)も、\(v(t) =\dot{x}(t)\)として決まることになる。我々はこれから、ダランベールの原理を使って、運動エネルギーとポテンシャルエネルギーの変化について追いかけたい。そこで、運動エネルギーの時間積分を考える。積分範囲は\(t_1\)から\(t_2\)までとしよう。

\[ \int_{t_1}^{t_2} K(v) dt \]

ただし、この積分は、運動方程式の解\((x(t),v(t))\)にそって実行するものとする。

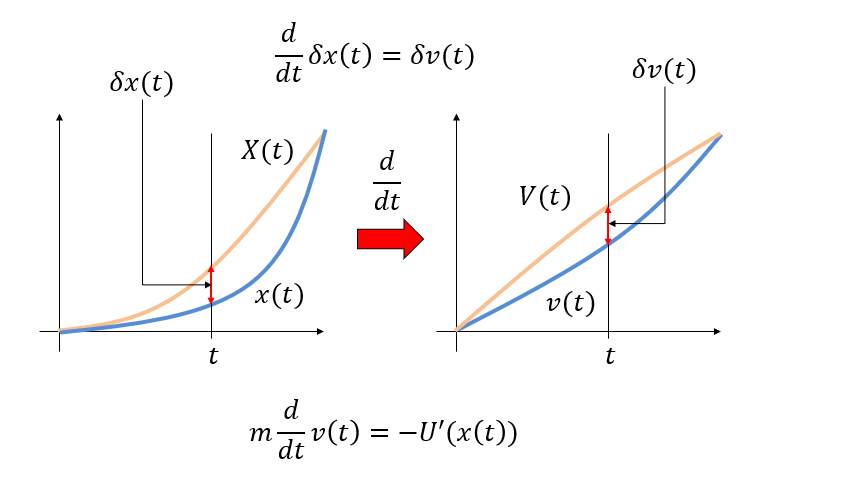
ここで、\(t=t_1\)と\(t=t_2\)における位置と速度\((x(t), v(t))\)を固定したまま、運動が少しずれた経路 \(X(t) = x(t) + \delta x(t)\)を辿ったと仮定する。ここで、\(\delta x(t)\) は時間依存する仮想変位である。\(X(t)\) は時間の関数であるから、時間微分することで少しずれた経路における速度\(V(t)\)が得られる。それを

\[ V(t) = v(t) + \delta v(t) \]

と書くと、

\[ V(t) = \dot{X}(t) \]

であることから、

\[ \delta v(t) = \frac{d}{dt}\delta x(t) \]

が成り立つことがわかる。さて、経路がずれたときの、この時の運動エネルギーの変化分の積分値を計算してみよう。先ほど求めたように

\[ \delta K = mv \frac{d}{dt} \delta x \]

であったから

\[ \begin{aligned} \delta \int_{t_1}^{t_2} K dt &\equiv \int_{t_1}^{t_2} \delta K dt \\ &= \int_{t_1}^{t_2} m v \frac{d}{dt} \left(\delta x\right) dt \\ &= - \int_{t_1}^{t_2} m \frac{dv}{dt} \delta x dv \end{aligned} \]

ここで、最後に部分積分を用いた。さて、ダランベールの原理により、

\[ \delta U = - m \frac{dv}{dt} \delta x \]

であったから、

\[ \int_{t_1}^{t_2} \delta K dt = \int_{t_1}^{t_2} \delta U dt \]

以上から、

\[ \int_{t_1}^{t_2} \delta (K-U) dt = 0 \]

を得た。この式の意味を考えよう。いま、ラグランジアン\(L(x, v)\)を

\[ L(x, v) = K(v) - U(x) \]

で定義し、それを時間積分した量\(I\)を考える。

\[ I = \int_{t_1}^{t_2} L(x, v)dt \]

もし\((x(t), v(t))\)が運動方程式の解であるならば、上記の積分が、運動方程式の解の経路からの微小変化\(x(t) \rightarrow x(t) + \delta x(t)\)に対して一次のオーダーで変化がゼロ、すなわち、

\[ \delta I = \int_{t_1}^{t_2} \delta L = 0 \]

を満たすということである。

さて、静力学においては、位置に依存する力\(F(x)\)がゼロであるような位置\(x\)を探すという力の釣り合い問題、すなわち

\[ F(x) = 0 \]

を満たす\(x\)を探せ、という問題を、力の積分であるポテンシャルエネルギー

\[ U(x) = \int F(x) dx \]

を考え、

\(U(x)\)を最小にする\(x\)を探せ、という問題に読み替えた。

動力学でも同様に、ダランベールの原理から、運動方程式の解である\((x(t), v(t))\)を探せ、という問題が、

\[ L(x, v) = K(v) - U(x) \]

という量を考え、その時間積分の

\[ I = \int L(x, v) dt \]

の最小値を与えるような軌道\((x(t),v(t))\)を探す問題に帰着した。静力学では時間変化がなかったので積分変数は\(x\)であったが、動力学では位置と速度が変化するため積分変数は\(t\)となる。この量\(I\)を 作用 (action)、この積分を作用積分と呼び、作用積分を与えるような被積分関数\(L\)を ラグランジアンと呼ぶ。あるラグランジアンが与えられた時、物体の軌道\(x(t)\)は、この作用積分を最小にするように決まることを要請する。これを ハミルトンの原理 (Hamilton’s principle) もしくは 最小作用の原理 (least action principle) と呼ぶ。保存力に対するポテンシャル関数と対比し、ラグランジアンを運動ポテンシャルと呼ぶこともある。ここでは、ダランベールの原理を用いたが、最小作用の原理からオイラー・ラグランジュ方程式を直接導出する方法を次章で説明する。

ラグランジアンと運動方程式

運動方程式から、ダランベールの原理を用いてラグランジアンを導いた。逆に、ラグランジアンから運動方程式を作ることができる。一体かつ一次元の問題を考える。ポテンシャル力\(U(x)\)に支配された運動のラグランジアンは

\[ L(x, v) = \frac{1}{2}mv^2 - U(x) \]

であった。これを\(x\)、\(v\)の独立な関数とみなして、まずは\(x\)で偏微分しよう。

\[ \frac{\partial L}{\partial x} = - U'(x). \]

次に、\(v\)で偏微分する。

\[ \frac{\partial L}{\partial v} = mv. \]

ニュートンの運動方程式はもともと

\[ m \frac{dv}{dt} = -U'(x) \]

であったから、ラグランジアンで運動方程式を表現すると、

\[ \frac{d}{dt} \left(\frac{\partial L}{\partial v}\right) = \frac{\partial L}{\partial x}. \]

もしくは、右辺を左辺に移項して

\[ \frac{d}{dt} \left(\frac{\partial L}{\partial v}\right) - \frac{\partial L}{\partial x} = 0. \]

これを、オイラー・ラグランジュ(Euler-Lagrange)の式と呼ぶ。ニュートンの運動方程式を変形しただけであるから、本質的にはニュートンの運動方程式と等価な式であるが、後で見るようにこの形式で書いておくと変数変換が非常にやりやすくなる。

ここでは発見法的にラグランジアンと運動方程式の関係を導いたが、これはユークリッド座標でない場合には適用できない。一般の座標については、変分原理を用いて定式化される。変分原理については次章で扱う。

多自由度系のラグランジアン

本質的に一自由度系と同じことであるが、多自由度系におけるラグランジアンと運動方程式の関係も見ておこう。

三次元系におけるラグランジアンが以下のように与えられているとする。

\[ L(x,y,z,\dot{x},\dot{y},\dot{z}) = K(\dot{x},\dot{y},\dot{z}) - U(x,y,z) \]

ただし\(K\)は運動エネルギーであり、

\[ K(\dot{x}, \dot{y}, \dot{z}) = \frac{1}{2}m(\dot{x}^2+\dot{y}^2+\dot{z}^2) \]

で与えられるものとする。この系の自由度は\(3\)、すなわち配位空間は3次元であり、その空間は\(x,y,z\)で張られている。自由度\(x\)に対応する速度は\(\dot{x}\)であることを考え、ラグランジアンを\(\dot{x}\)で偏微分してから時間微分したものを左辺に、\(x\)で偏微分したものを右辺に配置すると、自由度\(x\)に関する運動方程式を得る。

\[ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) = \frac{\partial L}{\partial x} \]

\(L\)の中身を代入すると、以下のようになる。

\[ m \frac{d \dot{x}}{dt} = - \frac{\partial U}{\partial x} \]

これは、ユークリッド空間において、自由な質点がポテンシャル\(U\)に起因する保存力に従って運動する様子を表現している。すなわち、先程のラグランジアンはそのような運動を表現していた。全く同様な手続きで、自由度\(y\)や\(z\)についての運動方程式も求めることができる。すなわち、3つの自由度\(x,y,z\)が従う3本の運動方程式が、ただ1つのスカラー関数\(L(x, y,z, \dot{x}, \dot{y},\dot{z})\)から導かれた。

ここでは、ユークリッド空間における自由な質点の運動を記述したが、拘束条件があったり、極座標のような一般の座標でも全く同様に、ラグランジアン一つから必要な数の運動方程式を生み出すことができる。一般に、\(N\)自由度系を考える。この系の配位空間は、\(N\)個の一般化座標\(q^1, q^2, \cdots, q^N\)で記述されている。これは、例えば剛体振り子のように、拘束条件がある場合に、それを考慮したような変数で記述されている場合を含む。もしこの系のラグランジアン\(L(q^1, q^2, \cdots, q^N, \dot{q}^1,\dot{q}^2,\cdots, \dot{q}^N)\)が与えられたならば、この系の\(N\)本の運動方程式は、

\[ \frac{d}{dt} \left(\frac{\partial L}{\partial \dot{q}^i} \right) - \frac{\partial L}{\partial q^i} = 0 \quad (i=1,2,\cdots, N) \]

で与えられる。すなわち、たった一つのスカラー関数に\(N\)本の運動方程式の情報が含まれている。

極座標の例

ラグランジアンで記述すると変数変換に強くなる例として、二次元空間における自由運動を例に挙げよう。ラグランジアンは、運動エネルギーとポテンシャルエネルギーの差を取れば良い。今回は自由運動を考えるのでポテンシャルエネルギーはゼロである。ユークリッド座標\((x,y)\)で記述すると運動エネルギーは、

\[ K(\dot{x},\dot{y}) = \frac{1}{2}m(\dot{x}^2+\dot{y}^2) \]

で与えられる。ここで、

\[ \begin{aligned} x &= r\cos\theta \\ y &= r\sin\theta \end{aligned} \]

により極座標を導入する。両辺を時間微分して自乗和を取ると、極座標における運動エネルギーの表現

\[ K(\dot{r},\dot{\theta}) = \frac{1}{2}m(\dot{r}^2+r^2\dot{\theta}^2) \]

が得られる。ここからオイラー・ラグランジュ方程式を用いると、ユークリッド座標の場合の運動方程式は以下のように求められる。

\[ \begin{aligned} \frac{d}{dt} \left(\frac{\partial L}{\partial \dot{x}} \right) - \frac{\partial L}{\partial x} &= m\ddot{x} =0 \\ \frac{d}{dt} \left(\frac{\partial L}{\partial \dot{y}} \right) - \frac{\partial L}{\partial y} &= m\ddot{y} =0 \end{aligned} \]

同様に、極座標の場合は以下のように計算される。ここで、ポテンシャルエネルギーがゼロであっても\(\partial_r L \neq 0\)であることに注意すること。

\[ \begin{aligned} \frac{d}{dt} \left(\frac{\partial L}{\partial \dot{r}} \right) - \frac{\partial L}{\partial r} &= m(\ddot{r} - r\dot{\theta}^2)=0 \\ \frac{d}{dt} \left(\frac{\partial L}{\partial \dot{\theta}} \right) - \frac{\partial L}{\partial \theta} &= m\frac{d}{dt}\left(r^2 \dot{\theta} \right) =0 \end{aligned} \]

このように、オイラー・ラグランジュ方程式は一般の変数変換に対して共変であるため、ラグランジアンを経由すると変数変換が非常に簡単にかける。ラグランジアンが一般の変数変換に対して共変である証明は後に与える。

まとめ

仮想仕事の原理では、位置の関数である力についてその原始関数であるポテンシャル関数を考え、そのポテンシャル関数が最小になるような点として釣り合いの点が決まると考えて定式化した。これを動力学に拡張するため、まずにより慣性項と力を同一視し、そこに仮想仕事の原理を適用した(ダランベールの原理)。しかし、一般に力は位置だけの関数であることが多いが、慣性項のポテンシャルに対応する運動エネルギーは一般に速度の関数となる。そこで、両者が依存する時間に対して積分した量をポテンシャルとして考え、それを最小にするように運動が決まると考える。この時、位置も速度も変化するが、速度が位置の時間微分であるという条件から部分積分することで、動力学におけるポテンシャルであるラグランジアンを導出した。ラグランジアンを(適切な境界条件のもと)時間積分したものが最小になるように運動が決まる、という主張がハミルトンの原理であり、そこから導出された運動方程式がオイラー・ラグランジュ方程式である。ラグランジアンはポテンシャルエネルギーを発展させた概念であり、運動エネルギーも含むことで多自由度系の運動方程式の情報をただ一つのスカラー関数に押し込めることができてる。これにより、変数変換や近似の見通しがよくなる。しかし、このような実用的な側面よりも、どんなに多自由度であっても、(そのようなラグランジアンを見つけることができれば)ただ一つのスカラー関数が運動を支配しているという不思議な事実を知ることが解析力学の醍醐味であろう。