[Up] [Repository]

解析力学を学ぶ前に、ニュートンの運動方程式がどのような性質を持っているかを確認しよう。まず、ニュートン力学について復習し、次にニュートンの運動方程式がガリレイ変換に対する共変性を持っていることを確認する。そのために、反変ベクトル、共変ベクトルの区別について学び、その後、座標変換に対する運動方程式の共変性について調べる。

力学の復習

原理と法則

これまでに力学を学んだはずである。これから学ぶ解析力学と区別するため、これまでに学んだ力学をニュートン力学と呼ぼう。ニュートン力学は「慣性の法則」「運動の法則」「作用・反作用の法則」の、運動の三法則を原理とする。「法則を原理とする」という言葉により、この三法則は原理なのか法則なのか混乱するかもしれない。ここで法則と原理について定義しておこう。

まず、物理において 法則 (law) とは観測事実である。様々な実験により、一般的に成り立っていると信じられる事実を法則と呼ぶ。例えばケプラーが太陽系について発見した、

• ケプラーの第一法則：惑星は太陽を焦点とする楕円軌道を描く
• ケプラーの第二法則：惑星と太陽を結ぶ線分が単位時間に描く面積は一定である
• ケプラーの第三法則：惑星の公転周期の2乗は、軌道長半径の3乗に比例する

などが法則の例である。これはケプラーが、ティコ・ブラーエの残した天文観測データから発見したものだ。すなわち観測事実である。

ニュートンは、ケプラーの残したデータから、「物体の間には互いに引き合う力が存在し、その力は質量に比例し、距離の2乗に反比例する」という万有引力の法則を発見する。ニュートンの運動方程式と、万有引力の法則を組み合わせることで、ケプラーの三法則を導くことができる。

さて、観測事実である法則を説明するためには、別の根拠が必要になる。その根拠を説明するためには、また別の根拠が必要になる。このようなことを繰り返していくと、どこかで「これ以上遡ることができない、議論の出発点」に到達する。この議論の出発点のことを 原理 (principle) と呼ぶ。原理は、我々が議論の余地なく認めるもので、それさえ認めてしまえば、世界の様々な観測事実をうまく説明できるものだ。ニュートンは、様々な観測事実から、運動の三法則が成り立っていることを確信した。そこで、この三法則を原理として要請することで、ニュートン力学が構築された。

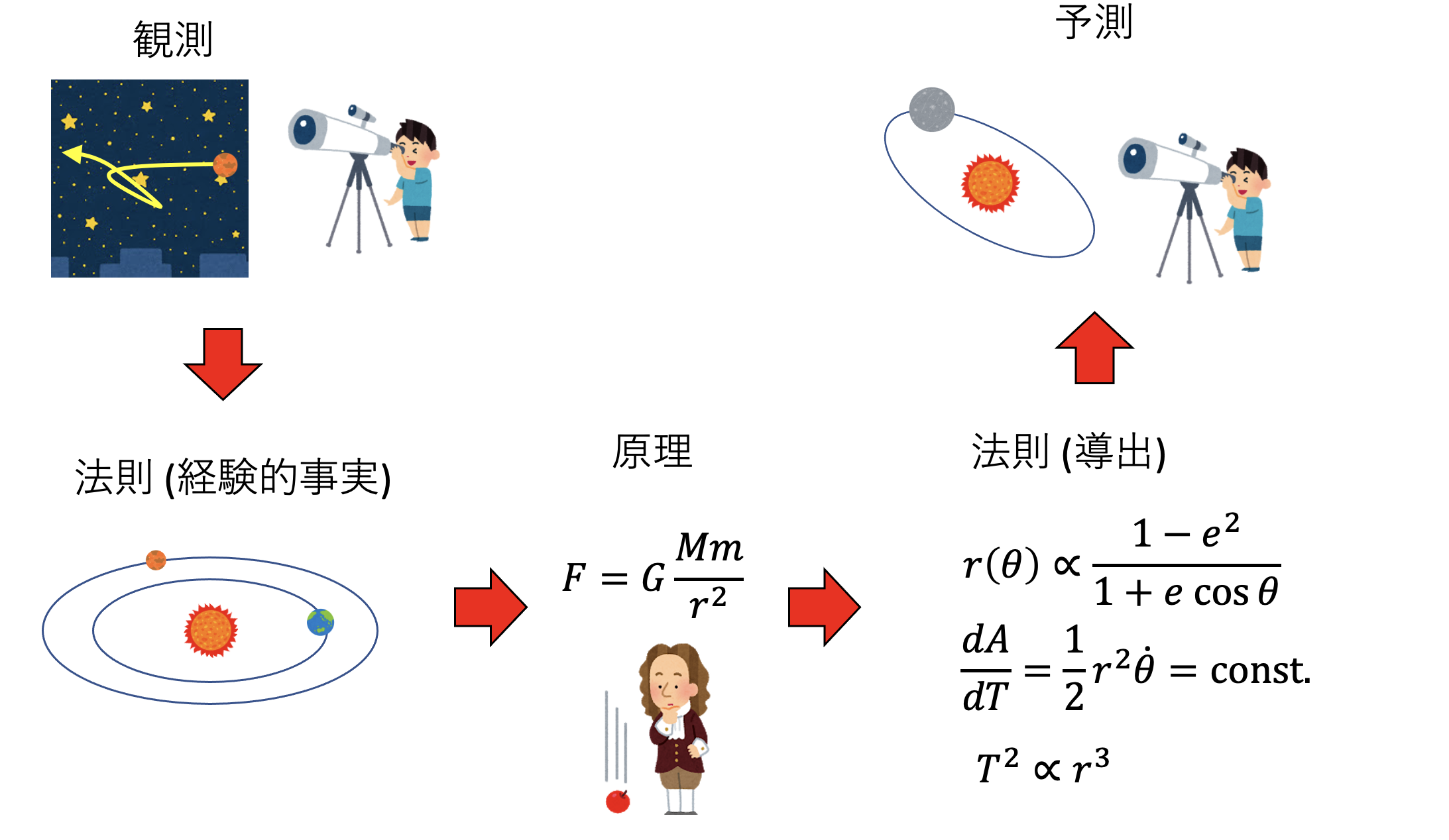
原理は議論の出発点であるから、原理が正しいことについて別に根拠を求めることができない。そこで、我々はその原理から導かれる知識を使って、何かを予測する。例えば、もしニュートン力学と万有引力が正しければ、未知の天体についてもその軌道を予測することができるはずだ。18世紀、火星と木星の間に大きな隙間があることが知られており、そこに未知の惑星があることが予想されていた。その惑星はケレスと名付けられ、1801年1月1日に発見されたが、その後、位置を見失っていた。ガウスはケレスの正確な位置を計算することに成功し、それにより同年12月31日、予測された位置でケレスは再発見された。このように、原理からの予測が未知の現象を説明できたならば、我々はその原理を正しいと信じていくことになる。この「観測事実→法則(経験的事実)→原理→法則(導出)→予測」という一連の流れは、物理学において極めて普遍的に見られる営みである。

運動の三法則

力学は物体の運動を扱う学問である。一般に物体は大きさを持つ。物体の質量が一点に集まっているとして運動が記述できる場合、その物体を質点と呼ぶ。物体の大きさが無視できないが、物体が十分に硬く、その変形が無視できる場合を剛体と呼ぶ。物体の変形まで考慮する場合、加えている力を取り除くと元に戻る物体を弾性体、変形が有限のまま残る物体を塑性体と呼ぶ。さらに、無限小の力で有限の変形を引き起こせる物体を流体と呼び、それを扱う学問が流体力学である。

本講義では、質点の運動のみを扱うことにする。なお、有限の大きさを持つ物体の運動も扱うが、その物体の回転などを扱わないため、質点の運動として記述できる。

さて、改めてニュートンの運動の三法則を見てみよう。

• 運動の第一法則(慣性の法則)
  • 他から力が働いていない質点は、等速直線運動を行う。
• 運動の第二法則(運動の法則)
  • 質点に力が働く時、質点は力の方向に、力に比例、質量に反比例する大きさの加速度を持つ。
• 運動の第三法則(作用・反作用の法則)
  • 2つの質点の間に力が働く時、両者の大きさは等しく、向きは逆向きとなる。

第一法則は、「他から力が作用していない質点は、等速直線運動をする」と表現される。質点が静止している場合も、速度ゼロの等速直線運動とみなす。これを慣性の法則と呼び、慣性の法則が成り立つ系を 慣性系 (inertial frame of reference) と呼ぶ。第一法則は、この慣性系が存在する(我々が慣性系を採用できる)ことを主張する。慣性系とは、ひらたく言えば「止まっている座標系」である。全ての運動はこの座標系から見た相対運動として表現することができる。第一法則は、しばしば第二法則の加速度がゼロの場合の特殊なケースであるとよく誤解されるが、第二法則は慣性系を定義しなければ意味を持たないため、第一法則とは別の法則である。

第二法則は、いわゆる\(F=ma\)を指す。しかし、質点の運動、特に加速度を定義するためには、「何に対して動いているのか」を考えなければならない。第二法則をより正確に記述するなら「質点に力が働く時、質点は 慣性系に対して 力の方向に、力に比例、質量に反比例する加速度を持つ」となる。加速度運動を定義するためには、静止した座標系が必要となる。第一法則は、その静止した座標系が定義できることを主張する。

ここで、静止した座標系と書いたが、実際には、ある静止した座標系に対して等速直線運動をしているような座標系もやはり慣性系となるため、こちらを「静止している」とみなすこともできる。ニュートンは絶対静止空間を考えたが、現在では特別な慣性系は存在せず、無数にある慣性系の中から計算に便利な慣性系を選んで採用していると解釈する。

第三法則は、力は必ずペアで、大きさが同じで、かつ逆向きに発生することを主張する。これは観測事実であり、なぜそうであるかは説明してくれない。今、第三法則を破る物体があるとしよう。たとえば同じ符号の電荷のように互いに反発するが、一方から一方への力が、逆向きに働く力よりも強いとする。すると、一方に力を加え、もう一方を間接的に動かすと、加えた力以上の力が得られることになる。これを利用して仕事を取り出すことが可能であるから永久機関を作ることができる(第一種永久機関)。第三法則はこのようなことができないことを主張する。

座標変換と運動方程式の共変性

同じ物体の運動を別の人が観測しているとする。それぞれの観測者は異なる座標から物体の運動を観測している。この時、観測者によって物理法則が異なるように見えては困る。そこで、どの観測者から見ても成立するような法則を物理法則と呼ぶことにする。これは、どこかに絶対的な代表がいて、その人にとっての運動法則だけが正しいわけではなく、全ての観測者は相対的であり、誰にとっても運動法則は同じように見えて欲しい、という要請である。この要請を相対性原理と呼ぶ。

力学は空間の中の物体の軌跡を追いかける学問であり、異なる座標系を用いれば、軌跡も異なって見える。その中で何が形を変えないものが物理法則である。そこで、座標変換によって物理法則がどのように変換されるかを知る必要がある。その準備として、座標変換によりスカラーやベクトルがどのように変換を受けるかを調べ、改めてスカラー、ベクトルを定義しよう。

スカラー

地図を思い浮かべて欲しい。地図には等高線が書いてあり、その場所での標高がわかるようになっている。この地図を使って、現在自分がいる地点の標高を調べたとしよう。さて、目的地に向かうため、道の方向に合わせて地図を向きを回転させたとしよう。これは座標変換したことに対応するが、座標変換しても現時点の高さは変わらない。このように、座標変換により変換を受けない量を スカラー(scolar) と定義する。

地図の例でいえば、座標\((x,y)\)に対して、高さ\(h(x,y)\)が定義されており、変数変換\((x,y)\rightarrow (\tilde{x}, \tilde{y})\)をしても、そこが同じ場所であるならば高さの値\(h(\tilde{x}, \tilde{y})\)は変わらないことを意味する。

ベクトル

座標変換により値が変わらないのがスカラーであった。一方、座標変換で値が変わるのがベクトルである。一般に、ベクトルは適当な基底を選ぶことで成分表示できる。同じベクトルでも、別の基底を選ぶと成分が変わる。この成分の変化のし方により、ベクトルは反変ベクトルと共変ベクトルに分類される。

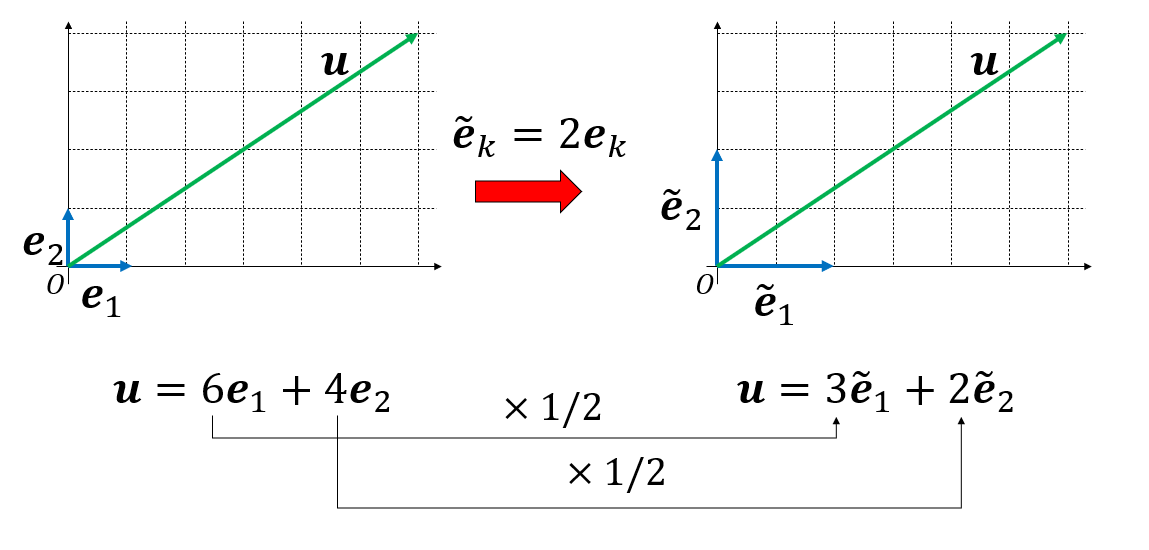
例を挙げよう。基底\(\{\mathbf{e}_1, \mathbf{e}_2\}\)で張られる二次元空間があり、あるベクトル\(\mathbf{u}\)がこの基底により

\[ \mathbf{u} = 6 \mathbf{e}_1 + 4 \mathbf{e}_2 \]

と展開されているとしよう。この時、ベクトルの成分表示は\(\mathbf{u} = (6,4)\)となる。さて、基底の長さを2倍にしてみよう。

\[ \begin{aligned} \tilde{\mathbf{e}}_1 &= 2 \mathbf{e}_1 \\ \tilde{\mathbf{e}}_2 &= 2 \mathbf{e}_2 \end{aligned} \]

新しい基底\(\{\tilde{\mathbf{e}}_1, \tilde{\mathbf{e}}_2\}\)で\(\mathbf{u}\)を展開すると、

\[ \mathbf{u} = 3 \tilde{\mathbf{e}}_1 + 2 \tilde{\mathbf{e}}_2 \]

となる。この時、ベクトルの成分表示は\(\mathbf{u} = (3,2)\)と、元の半分になる。このように、基底の長さを2倍にした時、成分が半分となるようなベクトルを、基底と反対向きの変換を受けるという意味で 反変ベクトル(contravariant vector) と呼ぶ。このように、基底で展開した成分は反変ベクトルとなる。反変ベクトルの正確な定義は後に与える。

この事実を一般化しておこう。いま、あるベクトル\(\mathbf{u}\)が正規直交基底\(\{\mathbf{e}_i\}\)により、以下のように成分表示されているとしよう。

\[ \mathbf{u} = u^i \mathbf{e}_i \]

さて、別の正規直交基底\(\{\tilde{\mathbf{e}}_i\}\)を考え、先ほどのベクトルが

\[ \mathbf{u} = \tilde{u}^i \tilde{\mathbf{e}}_i \]

と展開できるとしよう。さらに、二種類の基底が変換行列\(T\)を用いて

\[ \tilde{\mathbf{e}}_i = T^k_{\,i} \mathbf{e}_k \]

と結びついているとする。この時、この変換の前後のベクトルの成分\(u^i\)と\(\tilde{u}^i\)の間の関係を調べよう。

ベクトル\(\mathbf{u}\)を新しい基底\(\{\tilde{\mathbf{e}}_i\}\)で展開した式に、基底の変換の関係を代入する。

\[ \begin{aligned} \mathbf{u} &= \tilde{u}^k \tilde{\mathbf{e}}_k \\ &= \tilde{u}^k T^j_{\,k} \mathbf{e}_j \end{aligned} \]

両辺について\(\mathbf{e}^i\)と内積をとると、

\[ \begin{aligned} u^i &= \tilde{u}^k T^j_{\,k} (\mathbf{e}^i,\mathbf{e}_j),\\ &= \tilde{u}^k T^j_{\,k} \delta^i_{\,j}, \\ &= T^i_{\,k} \tilde{u}^k. \end{aligned} \]

基底の変換と並べてみると、

\[ \begin{aligned} \tilde{\mathbf{e}}_i &= T^k_{\,i} \mathbf{e}_k \\ u^i &= T^i_{\,k} \tilde{u}^k \end{aligned} \]

チルダが現れる項が左右逆になっていることがわかる。このように、\(\mathbf{u}\)は基底の変換と反対の変換を受けるので反変ベクトルと呼ばれる。

逆に、基底と同じ形の変換を受けるベクトル、すなわちチルダが同じ側に現れるのが共変ベクトルである。定義から、基底自身は共変ベクトルとなる。さらに、先程、反変ベクトルであることがわかった成分ベクトルを縦ベクトルとすると、その双対である横ベクトルは共変ベクトルとなる。

\(\{\mathbf{e}_i\}\)や\(\{\tilde{\mathbf{e}}_i\}\)が張っていた空間と双対な空間を張る基底\(\{\mathbf{e}^i\}\)や\(\{\tilde{\mathbf{e}}^i\}\)を考えよう。\(\{\mathbf{e}_i\}\)で張られる空間のベクトルを縦ベクトルとするので、\(\{\mathbf{e}_i\}\)と添字が下についている基底を縦ベクトルの基底と呼ぼう。すると、その双対ベクトル\(\{\mathbf{e}^i\}\)で展開されるベクトルは横ベクトルとなるため、\(\{\mathbf{e}^i\}\)と上付きの添字を持つ基底を横ベクトルの基底と呼ぶことにする。

以下のように、共役なベクトルとの直交性を課す。

\[ \begin{aligned} (\mathbf{e}^j,\mathbf{e}_i) &= \delta^j_{\,i} \\ (\tilde{\mathbf{e}}^j,\tilde{\mathbf{e}}_i) &= \delta^j_{\,i} \\ \end{aligned} \]

さて、縦ベクトルの基底が\(\tilde{\mathbf{e}}_i = T^k_{\,i} \mathbf{e}_k\)と変換される時、横ベクトルの基底がどのように変換されるか見てみよう。変換の前後で

\[ \tilde{\mathbf{e}}^i = M^i_{\,k} \mathbf{e}^k \]

と展開できるとする。両辺、\(\mathbf{e}_j\)との内積を取ると、

\[ \begin{aligned} (\tilde{\mathbf{e}}^i, \mathbf{e}_j) &= M^i_{\,k} (\mathbf{e}^k, \mathbf{e}_j) &= M^i_{\,k} \delta^k_{\,j} \\ &= M^i_{\,j} \end{aligned} \]

縦ベクトルの基底の変換は以下で与えられているとする。

\[ \tilde{\mathbf{e}}_i = T^k_{\,i} \mathbf{e}_k. \]

両辺、\(\tilde{\mathbf{e}}^j\)と内積をとると、左辺は直交性から

\[ (\tilde{\mathbf{e}}^j, \tilde{\mathbf{e}}_i) = \delta^j_{\,i}. \]

右辺は、先程求めた\((\tilde{\mathbf{e}}^i, \mathbf{e}_j) = M^i_{\,j}\)を代入することで

\[ T^k_{\,i} (\tilde{\mathbf{e}}^j, \mathbf{e}_k) = M^j_{\,k} T^k_{\,i} \]

以上から、

\[ M^j_{\,k} T^k_{\,i} = \delta^j_{\,i} \]

これは、行列表示すれば\(MT = I\)、すなわち行列\(M\)と\(T\)が互いに逆行列の関係にあることを意味する。

さて、横ベクトル\(\mathbf{v}\)が、横ベクトルの基底で

\[ \mathbf{v} = v_i \mathbf{e}^i = \tilde{v}_i \tilde{\mathbf{e}}^i \]

と展開されているとしよう。縦ベクトルと同様な議論から、

\[ v_k = M^j_{\,k} \tilde{v}_j \]

が成立する。両辺に行列\(T\)をかけると、

\[ \begin{aligned} T^k_{\,i} v_k &= T^k_{\,i} M^j_{\,k} \tilde{v}_j \\ &= \delta^j_{\,i} \tilde{v}_j \\ &= \tilde{v}_i \end{aligned} \]

縦ベクトルの基底の変換の式と並べると、

\[ \begin{aligned} \tilde{\mathbf{e}}_i &= T^k_{\,i} \mathbf{e}_k \\ \tilde{v}_i &= T^k_{\,i }v_k \end{aligned} \]

のように、基底の変換とベクトルの変換のチルダのある方が同じ側に来ることがわかる。このような変換をするベクトルを共変ベクトルと呼ぶ。すなわち、横ベクトルは縦ベクトルの基底変換に対して共変性を持つ。

さて、もともとの基底の変換則は以下で与えられていた。

\[ \tilde{\mathbf{e}}_i = T^k_{\,i} \mathbf{e}_k. \]

これを両辺転置してみよう。

\[ \begin{aligned} {}^t(\tilde{\mathbf{e}}_i) &= {}^t(T^k_{\,i} \mathbf{e}_k)\\ \tilde{\mathbf{e}}^i &= ({}^tT)^i_k \mathbf{e}^k \end{aligned} \]

ここで、

\[ \tilde{\mathbf{e}}^i = M^i_k \mathbf{e}^k \]

であったから、\({}^tT = M\)である。先程\(M=T^{-1}\)であることを証明したので、\({}^tT = T^{-1}\)、すなわち変換行列\(T\)は転置を取ると逆行列になることがわかる。この性質を持つ行列を直交行列、この行列による変換を直交変換と呼ぶ。このように、正規直交基底から正規直交基底へ変換する行列は直交行列となる。

解析力学においては線形でない基底変換も考慮するが、非線形な変換であってもある点の近傍で展開すれば線形変換とみなすことができる。非線形な座標変換の典型例がデカルト座標から極座標への変換である。例えば\((x,y)\)と\((r,\theta)\)の変換を考えよう。

\[ \begin{aligned} x &= r \cos\theta \\ y &= r \sin \theta \end{aligned} \]

この変換は非線形だが、全微分を考えると線形変換とみなすことができる。

\[ \begin{aligned} dx &= \cos \theta dr - r \sin \theta d\theta \\ dy &= \sin \theta dr + r \cos \theta d\theta \\ \end{aligned} \]

これは、基底\(\{dr, d\theta\}\)から、\(\{dx, dy\}\)への線形変換と見ることができる。後で見やすいように、\((r,\theta)\)を\((x^1,x^2)\)、\((x,y)\)を\(\tilde{x}^1, \tilde{x}^2\)と表記すると、先程の全微分の式は、

\[ d\tilde{x}^i = \frac{\partial \tilde{x}^i}{\partial x^k} dx^k \]

とまとめることができる。例えば

\[ \frac{\partial \tilde{x}_1}{\partial x_2} \equiv \frac{\partial x}{\partial \theta} \]

である。このように、座標の微分\(dx, dy\)や\(dr, d\theta\)は自然に反変ベクトルとなる。

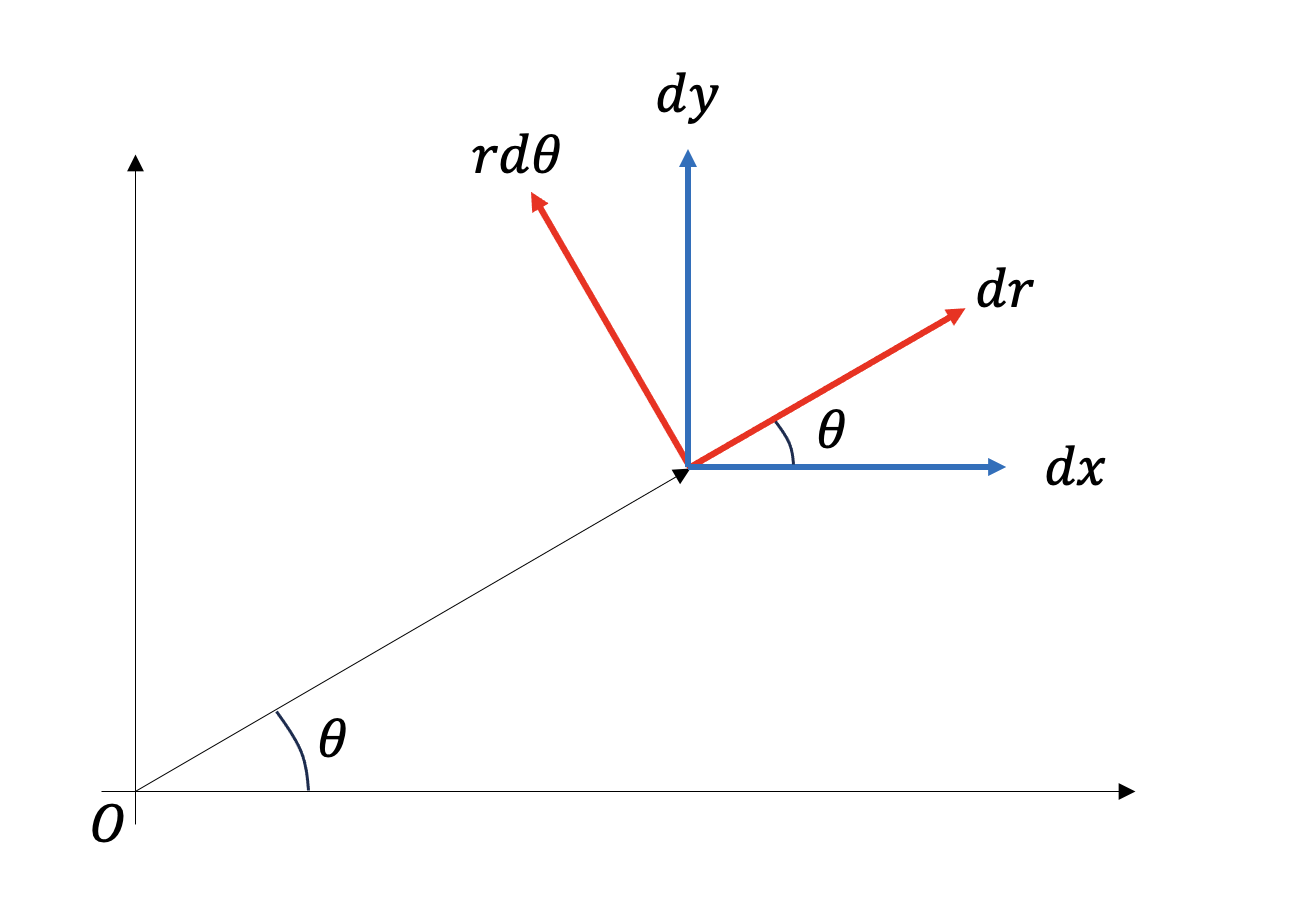
この変換がどのような幾何学的な意味を持つか見てみよう。二次元平面上の点\(P(\sqrt{3}/2, 1/2)\)を考える。この点における極座標変換を考えよう。点\(P\)における値を添え字\(P\)で表すと

\[ \begin{aligned} dx &= \left(\frac{\partial x}{\partial r}\right)_P dr +\left(\frac{\partial x}{\partial \theta}\right)_P dr \\ dy &= \left(\frac{\partial y}{\partial r}\right)_P dr +\left(\frac{\partial y}{\partial \theta}\right)_P dr \end{aligned} \]

点\(P\)において\((r, \theta) = (1, \pi/6)\)であるので、

\[ \begin{aligned} \left(\frac{\partial x}{\partial r}\right)_P &= (\cos \theta)_P = \frac{\sqrt{3}}{2} \\ \left(\frac{\partial x}{\partial \theta}\right)_P &= (-r \sin \theta)_P = -\frac{1}{2}\\ \left(\frac{\partial y}{\partial r}\right)_P &= (\sin \theta)_P = \frac{\sqrt{1}}{2} \\ \left(\frac{\partial y}{\partial \theta}\right)_P &= (r \cos \theta)_P = \frac{\sqrt{3}}{2} \end{aligned} \]

以上を行列形式でまとめると

\[ \begin{aligned} \begin{pmatrix} dx\\dy \end{pmatrix} &= \begin{pmatrix} \sqrt{3}/2 & -1/2 \\ 1/2 & \sqrt{3}/2 \end{pmatrix} \begin{pmatrix} dr \\ d\theta \end{pmatrix}\\ &= \begin{pmatrix} \cos(-\theta) & \sin(-\theta) \\ -\sin(-\theta) & \cos(-\theta) \end{pmatrix} \begin{pmatrix} dr \\ d\theta \end{pmatrix} \end{aligned} \]

これは、点\(P\)における\((-\theta)\)回転に他ならない。図を見れば、確かに\((dr, d\theta)\)が張る座標系を\(-\theta\)だけ回転させたものが\((dx, dy)\)が張る座標系になっていることがわかる。このように、どのような非線形変換であっても、適当な点の近傍で展開することで線形変換にすることができる。

一般に、\(\{x^i\}\)から\(\{\tilde{x}^i\}\)への非線形な座標変換において、

\[ \tilde{A}^i = \frac{\partial \tilde{x}^i}{\partial x^j} A^j \]

のように変換を受けるベクトル\(\mathbf{A}\)を反変ベクトルと定義し、添字を右上につける。チルダのある量を左辺に持ってきた時、右辺の変換行列の偏微分の分子にチルダが現れるのが反変ベクトルである。この変換公式が反変ベクトルの定義を与える。

逆に、

\[ \tilde{B}_i = \frac{\partial x^j}{\partial \tilde{x}^i} B_j \]

のように変換を受けるベクトル\(\mathbf{B}\)を 共変ベクトル (covariant vector) と呼び、添字を右下につける。チルダのある量を左辺に持ってきた時、右辺の変換行列の偏微分の分母にチルダが現れるのが反変ベクトルである。この変換公式が共変ベクトルの定義を与える。

数学的準備の章にて、\(dx\)を横ベクトルとみなすと、\(\partial_x\)が自然な双対基底であり、縦ベクトルとみなせることを見た。従って、\(\partial_x, \partial_y\)は共変ベクトルとなることが期待される。

いま、\((x^1, x^2)\)で張られる空間に、スカラー関数\(f(x^1, x^2)\)があるとしよう。この関数の勾配(gradient)が、変数変換\((x^1, x^2) \rightarrow (\tilde{x}^1, \tilde{x}^2)\)でどのように変換されるか見てみよう。合成関数の偏微分の公式から、

\[ \begin{aligned} \frac{\partial f}{\partial \tilde{x}^1} &= \frac{\partial f}{\partial x^1} \frac{\partial x^1}{\partial \tilde{x}^1}+ \frac{\partial f}{\partial x^2} \frac{\partial x^2}{\partial \tilde{x}^1}\\ \frac{\partial f}{\partial \tilde{x}^2} &= \frac{\partial f}{\partial x^1} \frac{\partial x^1}{\partial \tilde{x}^2}+ \frac{\partial f}{\partial x^2} \frac{\partial x^2}{\partial \tilde{x}^2}\\ \end{aligned} \]

これが任意の\(f\)について成り立つので、

\[ \tilde{\partial}_i = \frac{\partial x^k}{\partial \tilde{x}^i} \partial_k \]

ここで、\(\partial_i \equiv \partial_{x_i}\)、\(\tilde{\partial}_i \equiv \partial_{\tilde{x}_i}\)という表記を用いた。右辺に現れる偏微分の分母にチルダのある量が現れているため、\(\{\partial_i\}\)は共変ベクトルであることがわかる(そのため、添字を下に書いている)。

二つ並べると共変性、反変性がわかりやすい。

\[ \begin{aligned} d\tilde{x}^i &= \frac{\partial \tilde{x}^i}{\partial x^k} dx^k\\ \tilde{\partial}_i &= \frac{\partial x^k}{\partial \tilde{x}^i} \partial_k \end{aligned} \]

チルダなしの量からチルダ付きの量に変換した時、偏微分の上下どちらにチルダが現れるかが逆になっていることがわかる。このように、座標変換により変換を受ける量を一般にベクトル、変換を受けない(値が変わらない)量をスカラーと呼ぶ。

反変ベクトルと共変ベクトルは、スカラーを掛けたり割ったりしても反変性や共変性は変わらない。微分は割り算の極限として定義されるから、スカラーによる微分でも反変性や共変性は変わらない。また、反変ベクトルと共変ベクトルは内積を取ることでスカラー量となる。また、ベクトルが等式で結ばれている時、片方が反変ベクトルであるなら、もう片方も反変ベクトルでなければならない。

ニュートンの運動方程式の共変性

物理学は自然法則を記述する学問である。何かの現象を記述する際、どのような座標系を選ぶかは任意であるから、物理法則が座標系に依存してはならない。一般に速度や位置はベクトル量であるから座標変換によりその値を変えるが、その関係を示す運動法則は変わってはならない。このような性質を 共変性(covariance) と呼ぶ。以下では、ニュートンの運動方程式が座標変換に対してどのように変換を受けるか見てみよう。

ニュートンの運動方程式は以下のように書ける。

\[ m \ddot{\mathbf{r}} = \mathbf{F} \]

ただし、

\[ \mathbf{r} = x^i \mathbf{e}_i \]

である。

ここで、以下のような\(\{\mathbf{e}_i\}\)から\(\{\mathbf{\tilde{e}}_i\}\)への変換を考える。

\[ \tilde{\mathbf{e}}_i = T^k_{\,i} \mathbf{e}_k \]

ただし、\(\{\mathbf{e}_i\}\)及び\(\{\mathbf{\tilde{e}}_i\}\)は正規直交基底であるとする。すると、変換行列\(T\)は直交行列となるため、

\[ {}^t T= T^{-1} \]

を満たす。

既に見たように、位置ベクトルは反変ベクトルであり、以下の様に変換される。

\[ x^i = T^i_j \tilde{x}^j \]

両辺を\(\tilde{x}^j\)で偏微分すると、

\[ T^i_j = \frac{\partial x^i}{\partial \tilde{x}^j} \]

である。

ここで、力が保存力であるとしよう。すると、ポテンシャル\(V(\mathbf{r})\)が存在し、力は以下のように書ける。

\[ \mathbf{F} = - \nabla V \]

力は座標による微分であるから、座標とは反対の変換を受けると予想される。実際に成分表示してみよう。

\[ F_i = - \frac{\partial V}{\partial x^i} \]

ここで、

\[ \tilde{F}_i = - \frac{\partial V}{\partial \tilde{x}^i} \]

という量を考えると、

\[ \begin{aligned} \tilde{F}_i &= - \frac{\partial V}{\partial \tilde{x}^i}\\ &= - \frac{\partial x^j}{\partial \tilde{x}^i}\frac{\partial V}{\partial x^j} \\ &= T^j_i F_j \end{aligned} \]

これは共変ベクトルの定義である。

座標の変換則

\[ x^i = T^i_j \tilde{x}^j \]

について、両辺に\(T^{-1}\)をかけると、

\[ \tilde{x}^i = (T^{-1})^i_j x^i \]

\({}^t T = T^{-1}\)であったから、

\[ \tilde{x}^i = T^j_i x^j \]

従って、

\[ m\ddot{\tilde{x}^i} = m T^i_j \ddot{x^i} \]

以上から、

\[ \begin{aligned} m\ddot{\tilde{x}^i} - \tilde{F}_i &= T^j_i (m \ddot{x}^j - F_j) \end{aligned} \]

従って、\(m \ddot{x}^j - F_j = 0\) が成り立つなら、\(m\ddot{\tilde{x}^i} - \tilde{F}_i\)=0$ も成り立つ。すなわち、ニュートンの運動方程式は直交変換に対して共変である。このように、何かが変換に対して共変であることを示したいとき、成り立つべき式がゼロとなるような形を作っておき、右辺がゼロなので左辺もゼロ、という論法をよく使うので気に留めておくとよい。

ここで、 共変性(covaiance) は 不変性(invariance) とは異なることに注意したい。例えばスカラー量は座標変換で値そのものを変えないので不変(invariant)である。一方、運動方程式は、座標変換によりベクトルの値は変更を受けるが、形を変えない。従って、線形変換で移ることができる異なる座標系に住む人にとって、同じ形の法則が成り立つ。これを共変(covariant)であると呼ぶ。

同様に、ニュートンの運動方程式はある座標に対して等速直線運動する座標系から見ても形を変えない。これは、以下の座標変換に対応する。

\[ \tilde{\mathbf{x}} = \mathbf{x} + \mathbf{u}t + \mathbf{c} \]

ただし\(\mathbf{u}\)は定ベクトルである。この変換を ガリレイ変換(Galilean transformation) と呼ぶ。

両辺を時間微分すると

\[ \tilde{\mathbf{v}} = \mathbf{v} + \mathbf{u} \]

両辺に質量\(m\)をかけて、さらに時間微分すると

\[ m \dot{\tilde{\mathbf{v}}} = m\dot{\mathbf{v}} \]

運動量の時間微分が形を変えないため、(力が時間や速度を陽に含まない限り)運動方程式も同じ形となることがわかる。

ニュートンの運動方程式は直交変換及びガリレイ変換に対して共変である。ガリレイ変換は、ある慣性系に対して加速度を持たない別の慣性系への座標変換を表現している。ニュートンの運動方程式がガリレイ変換により共変であるとは、ニュートンの運動方程式がすべての慣性系において同じ形をしていることを意味する。これは逆に、「どの慣性系から見ても同じ運動法則が成り立つようにニュートンの運動方程式が構成されている」と考えることもできる。「どの慣性系から見ても同じ運動法則が成り立つ」という要請をガリレイの相対性原理と呼ぶ。一方、電磁場の基礎方程式であるマクスウェルの方程式は、ガリレイ変換に対して共変ではないが、ローレンツ変換に対して共変性を持つ。ローレンツ変換において、物体の速度が光速に対して無視できるという近似をするとガリレイ変換に帰着する。アインシュタインは運動方程式やマクスウェル方程式を含む全ての物理法則が、あらゆる慣性系から同じように見えなければならないという原理を要請することで、特殊相対性理論を用いた。この要請を特殊相対性原理と呼ぶ。

ニュートンの運動方程式が直交変換及びガリレイ変換で共変であることを見たが、一般の変換に対しては共変ではない。簡単な例として、一次元空間の保存力による運動

\[ m \ddot{x} = F = - \frac{dU}{dx} \]

を考えよう。いま、座標を定数倍する\(\tilde{x} = a x\)という変換を考える。運動方程式の左辺は

\[ m \ddot{\tilde{x}} = a m \ddot{x} \]

という変換を受ける。一方、右辺は

\[ \begin{aligned} \tilde{F} &= -\frac{dU}{d\tilde{x}}\\ &= \underbrace{-\frac{dU}{dx}}_{F} \underbrace{\frac{dx}{d\tilde{x}}}_{1/a} \\ &= \frac{1}{a}F \end{aligned} \]

つまり、\(m\ddot{x} = F\)が成り立っていても、\(m\ddot{\tilde{x}} = \tilde{F}\)は成立しない。このように、直交変換でない変換についてはニュートンの運動方程式は共変ではない。極座標への変換も、ニュートンの運動方程式が共変でない座標変換である。極座標はよく使うので、運動方程式が共変でないといろいろ面倒だ。そこで、より広いクラスの変換に対して共変な運動方程式を使いたくなる。それが後に学ぶラグランジュ形式や、ハミルトン形式の運動方程式である。

保存則

ニュートンの運動方程式から得られる帰結として、いくつかの保存則を発見法的に導いておこう。

エネルギー保存則

バネでつながれた質点の運動方程式を考えよう。

\[ m \frac{d^2 x}{dt^2} = - kx \]

以下、面倒なので微分をドットで表現する。両辺に\(x\)の時間微分、すなわち速度をかける。

\[ m \dot{x} \ddot{x} = - k x \dot{x} \]

この式の左辺を眺めると、 \(m\dot{x}^2/2\) を時間微分したものであることがわかる。同様に右辺も\(-kx^2/2\)を時間微分したものである。そこで、

\[ \frac{d}{dt}\left(\frac{1}{2}m\dot{x}^2 \right) = - \frac{d}{dt}\left( \frac{1}{2} k x^2\right) \]

右辺を左辺に移行すると、

\[ \frac{d}{dt}\left(\frac{1}{2}m\dot{x}^2 + \frac{1}{2} k x^2\right) =0 \]

すなわち、運動方程式

\[ m \frac{d^2 x}{dt^2} = - kx \]

に従う系には、必ず時間不変量

\[ E = \frac{1}{2}m\dot{x}^2 + \frac{1}{2} k x^2 \]

が存在する。微分方程式において、時間不変量、すなわち時間微分してゼロとなる量を 保存量(Conserved value) と呼ぶ。この\(E\)をエネルギーと呼び、エネルギーが時間変化しないことをエネルギー保存則と呼ぶ。すなわち、エネルギーとは運動方程式の保存量の一つであり、エネルギー保存則は運動方程式の持つ性質の一つに過ぎない。

ここで、

\[ -kx = - \frac{d}{dx} \left( \frac{kx^2}{2}\right) \]

であることに注意しよう。このように、力\(F(x)\)がスカラー関数\(U(x)\)を使って

\[ F(x) = -U'(x) \]

と書ける時、このスカラー関数をポテンシャル、この力を保存力と呼ぶ。運動方程式の力が全てポテンシャルから引き出される場合、すなわち運動方程式が以下のような形をしている時、

\[ m\ddot{x} = -U'(x) \]

先程と全く同様に両辺に\(\dot{x}\)をかけることにより、以下のエネルギーが保存することを示すことができる。

\[ E = \frac{1}{2} m \dot{x}^2 + U(x) \]

このうち、右辺第一項を 運動エネルギー(Kinetic Energy) と呼び、\(K\)で表すことが多い。左辺第二項を ポテンシャルエネルギー(Potential Energy) と呼び、\(U\)で表すことが多い。一般的、物体に働く力が全てポテンシャルから引き出される場合、運動エネルギーとポテンシャルエネルギーの和である全エネルギーが必ず保存量となる。

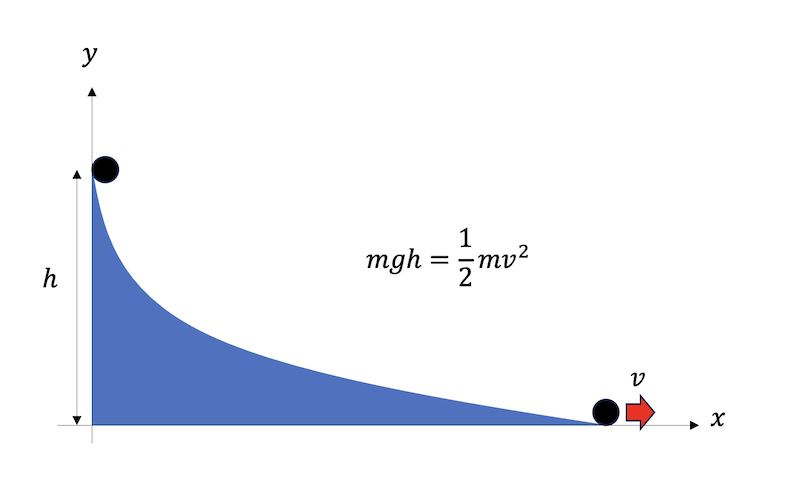
エネルギー保存則を用いると、微分方程式を明示的に解くことなく問題が解ける場合がある。例えば摩擦のない斜面で静止させていた物体の手を離し、物体が高さ\(h\)だけ滑りおりてから水平運動を始めたとする。水平運動の場合と比べて、静止時のポテンシャルエネルギーは\(mgh\)だけ高く、かつ静止時には運動エネルギーはゼロであるから、水平運動の速度を\(v\)とすると、エネルギー保存則より

\[ \frac{1}{2}mv^2 = mgh \]

であり、ここから速度を求めることができる。当たり前だと思うであろうが、ここで斜面の形状の情報を全く使っていないことに注意。斜面の形状を変えると、落下を開始してから高さ\(h\)だけ落ちるまでの時間が変化する。にもかかわらず、斜面がどのような形状であったとしても、最終的な速度は高さの差にしか依存しないことをエネルギー保存則は主張する。

ここで、エネルギーは運動方程式から発見法的に求められた保存量であったが、解析力学ではこの量を積極的に使って理論を構築する。

運動量保存則

3次元空間に質量\(m\)の質点A, Bがある。これらの質点の座標をそれぞれ\(\mathbf{r}_A = (x_A,y_A,z_A), \mathbf{r}_B = (x_B,y_B,z_B)\)とする時、これらが相対距離\(r\)に依存するポテンシャル\(U(r)\)により相互作用をしているとしよう。ただし\(r\)は以下のように定義する。

\[ \begin{aligned} r &= \sqrt{(\mathbf{r}_A -\mathbf{r}_B})^2\\ &= \sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2} \end{aligned} \]

この時、質点Aの運動方程式は、

\[ m \ddot{x}_A = - \frac{\partial U(r)}{\partial x_A} = - \frac{dU}{dr} \frac{\partial r}{\partial x_A} \]

で与えられる。従って、\(r\)を\(x_A\)で偏微分した結果が欲しい。

\[ r^2 = (x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2 \]

であったから、両辺を\(x_A\)で偏微分すると

\[ \frac{\partial r}{\partial x_A} = \frac{(x_A-x_B)}{r} \]

以上から、質点Aの運動方程式は

\[ m \ddot{x}_A = - U' \frac{(x_A-x_B)}{r} \]

全く同様に、\(r\)の\(x_B\)偏微分は

\[ \frac{\partial r}{\partial x_B} = - \frac{(x_A-x_B)}{r} \]

となるので(負符号がつくことに注意)、質点Bの運動方程式は

\[ m \ddot{x}_B = U' \frac{(x_A-x_B)}{r} \]

となる。\(y, z\)方向も同様である。従って、質点AB間に働く力は、大きさは同じで向きは逆向きとなり、作用・反作用の法則が成り立っていることがわかる。このように、相対座標のみに依存するポテンシャルによる相互作用は、作用・反作用の法則を自動的に満たす。

さて、力の大きさが同じで、向きが逆向きであるから、それぞれの運動方程式の和をとると、

\[ m (\ddot{x}_A+\ddot{x}_B) = 0 \]

となる。この系の\(x\)方向の重心位置\(x_G = (x_A + x_B)/2\)を定義すると、重心速度は\(\dot{x}_G\)であり、重心の運動量\(p_x = m \dot{x}_G\)を定義すると、\(\dot{p}_x = 0\)であることがわかる。\(y,z\)方向も同様であり、重心の運動量が保存することがわかる。

角運動量保存則

3次元空間に質点があり、その座標を\((x,y,z)\)とする。原点からの距離\(r = \sqrt{x^2+y^2+z^2}\)にのみ依存するポテンシャル\(U(r)\)に従って運動している時、角運動量が保存することを示そう。

まず、

\[ \begin{aligned} \frac{\partial r}{\partial x} &= \frac{x}{r} \\ \frac{\partial r}{\partial y} &= \frac{y}{r} \\ \frac{\partial r}{\partial z} &= \frac{z}{r} \end{aligned} \]

であることに注意する。この系の運動方程式は

\[ \begin{aligned} m \ddot{x} &= - U'(r) \frac{x}{r} \\ m \ddot{y} &= - U'(r) \frac{y}{r} \\ m \ddot{z} &= - U'(r) \frac{z}{r} \end{aligned} \]

\(m x\ddot{y} - m y \ddot{x}\)を計算すると、右辺が消えて、

\[ m x\ddot{y} - m y \ddot{x}= 0 \]

\(m\dot{x} \dot{y} - m\dot{x} \dot{y}\)を足すと、

\[ m \left(x\ddot{y} + \dot{x} \dot{y} - \dot{x} \dot{y} - y \ddot{x}\right) = 0 \]

この式をじっと眺めると

\[ m \frac{d}{dt}\left( x\dot{y} - y \dot{x} \right) =0 \]

ここで、\(x-y\)平面における角運動量

\[ L_z = m (x \dot{y} - y\dot{x}) \]

を定義すると、

\[ \dot{L}_z = 0 \]

であるから、\(L_z\)が保存量になることがわかる。同様に、

\[ \begin{aligned} L_x &= m (y \dot{z} - z\dot{y})\\ L_y &= m (z \dot{x} - x\dot{z})\\ \end{aligned} \]

も保存量となる。ここで、位置ベクトルと運動量ベクトル、角運動量ベクトルをそれぞれ

\[ \mathbf{r} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} , m\mathbf{v} = m \begin{pmatrix} \dot{x} \\ \dot{y} \\ \dot{z} \end{pmatrix} , \mathbf{L} = \begin{pmatrix} L_x \\ L_y \\ L_z \end{pmatrix} \]

と定義すると、角運動量ベクトルは

\[ \mathbf{L} = \mathbf{r} \times m\mathbf{v} \]

と表すことができ、角運動量保存則は

\[ \frac{d}{dt}\mathbf{L} = \mathbf{0} \]

とまとめることができる。

ニュートンの運動方程式のまとめ

本章では、ニュートンの運動方程式について復習した。物理学の使命は観測事実を説明することである。そのために観測結果から経験事実である法則を導き、その法則を導出できるような原理を発見し、逆に原理から理論を構築し、まだ見ぬ結果を予測する、というサイクルを繰り返していく。そうして生まれた理論の一つがニュートン力学である。ニュートン力学の根幹はニュートンの運動方程式であり、ニュートンの運動方程式はガリレイ変換に対して共変であったが、より一般の座標変換、たとえば極座標への変換では共変ではなかった。また、運動エネルギー、運動量、角運動量は、特定の条件を満たすような運動方程式における時間不変量であった。それらが保存することを導く際、両辺に速度をかけたり、ゼロとなる量を足したり引いたりした上に、式をじっと眺めて時間微分の形に持っていくなど、発見法的な方法に頼っていた。もっとシステマティックに保存量を見つけることはできないだろうか？また、保存量が存在するような特定の条件とはどのようなものであろうか？これらに答えを与えるのがこれから学ぶ解析力学である。

余談：リンゴに働く力

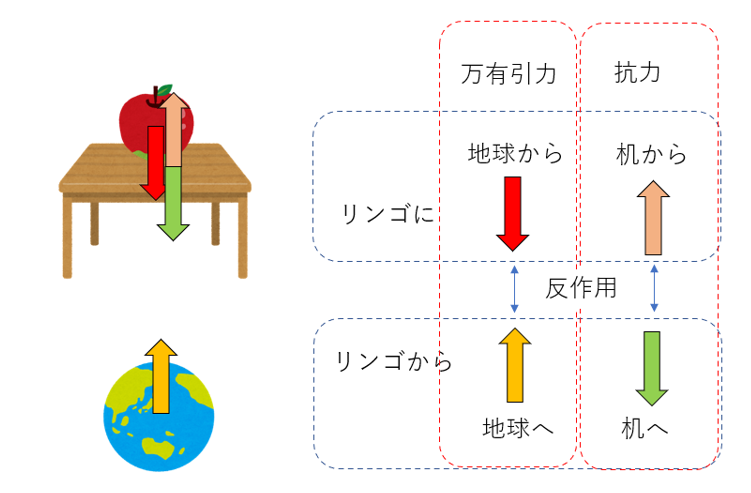
机の上にリンゴが乗っている。リンゴに働く力は重力と机からの抗力である。では、リンゴに働く重力の反作用は何か？

正解は、リンゴが地球を引っ張る力である。作用反作用の法則が「2つの質点の間に力が働く時、両者の大きさは等しく、向きは逆向きとなる」であり、リンゴに働く重力と抗力が大きさは等しく、向きが逆向きであることから、うっかり、机からの抗力と答えてしまいがちである。

リンゴが静止している以上、リンゴに働く力は釣り合っている。リンゴには重力と抗力しか働いておらず、力が釣り合っているのであるから、それらは同じ大きさで逆向きでなければならない。しかし、これは力の釣り合いである。作用・反作用の法則は、あくまでも力を及ぼし合う 二つの物体 の間に働く関係であり、重力がリンゴと地球の間に働く力である以上、リンゴに働く重力の反作用はリンゴが地球をひっぱる力でなければならない。抗力はリンゴと机の間に働く力であり、机からの抗力と同じ力でリンゴが机を押している。リンゴは机を押しているから、リンゴを載せる前に比べて、机はリンゴの重さだけ重くなっている。

同様な問いに、「重量計の上に密閉されたガラスケースがあり、その中にラジコンヘリコプターがある。ラジコンを操作してケースの中のラジコンを空中で静止させた時、飛ばす前に比べて重量計の指す値は大きくなるか？」というものがある。これも作用反作用の法則で説明ができるが、正答できるだろうか？