FDPSを使ってみるその4

はじめに

粒子系の並列シミュレーションフレームワークFDPSを使ってみる。その3では理想気体の並列計算、領域分割までおこなった。今回は、相互作用を入れた計算を試みる。まずは並列化しないシリアル版で、二粒子がお互いに正面衝突して離れていく過程を計算し、全エネルギー及び運動量が保存されていることを確認する(基本)。

コードはここにおいてある。 https://github.com/kaityo256/fdps_sample

FDPSの仕様書(PDF)はFDPSのGithubディレクトリにおいてあるのでそれを参照。

相互作用計算用のツリー

相互作用を計算するためのツリーを定義する。ツリーの探索モードは仕様書の6.6節にある。これから計算するのは全ての粒子が同じカットオフを持つ短距離相互作用Lennard-Jones粒子系なので、「相互作用の到達距離が有限でかつ、その到達距離がi粒子で決まる」場合、すなわち、PS::SEARCH MODE GATHERに対応すると思われる。

ツリーの定義には、力の計算結果格納用のForceクラス、i粒子を表すEssentialParticleIクラス、j粒子を表すEssentialParticleJクラスが必要となる。しかし、Lennard-Jones系ではどちらも同じクラスにしてしまってかまわないので、どちらもEPLJクラスとしてしまおう。とりあえず中身が空のまま定義して、あとで中身を記入していくことにする。

class ForceLJ {
};
class EPLJ {
};
PS::TreeForForceShort<ForceLJ, EPLJ, EPLJ>::Gather tree_lj;

これでコンパイルが通ることを確認しておく。

次にツリーを初期化する。必須のパラメタは最大粒子数。今回は二粒子系を扱うので2を入れる。

  const int N = 2;
  tree_lj.initialize(N);

相互作用計算の準備

相互作用はツリーを用いて計算する。最終的に

tree_lj.calcForceAllAndWriteBack(CalcForceLJ(), lj_system, dinfo);

のコンパイルが通ることを目標に、先程書いた空っぽのクラスの中身を埋めていく。

まず、力を定義するクラス(計算した結果を格納するクラス)は、計算した力、後でついでに計算するポテンシャルエネルギー、そして力を積算せずクリアするためのclear()が必要となる。こんな感じ¹。

class ForceLJ {
  public:
  PS::F64vec force;
  PS::F64 potential;
  void clear() {
    force = 0.0;
    potential = 0.0;
  }
};

次に、粒子を定義していたFPLJクラスに、力の書き戻しを受け取るメソッドが必要になる。ついでにあとで必要になるidや、ポテンシャルエネルギーを受け取るためのpotentialも追加しておく。

class FPLJ {
public:
  PS::S32 id; //追加
  PS::F64vec p;
  PS::F64vec q;
  PS::F64vec force; //追加
  PS::F64 potential;
  PS::F64vec getPos() const {
    return q;
  }
  void setPos(PS::F64vec nq) {
    q = nq;
  }
  // 以下を追加
  void copyFromForce(const ForceLJ & f) {
    force = f.force;
    potential = f.potential;
  }
};

EssentialParticleクラスにも、IDや、座標、setter, getter、FPLJクラスからの情報受け取りメソッドcopyFromFPなどが必要になる。もう一つ重要なのは、探索範囲を示すgetRSearch()。LJ系では定数なので、グローバル定数を返すことにしよう。

const PS::F64 CUTOFF_LENGTH = 3.0;
class EPLJ {
  public:
  PS::S32 id;
  PS::F64vec q;
  PS::F64vec getPos() const {
    return q;
  }
  void setPos(const PS::F64vec & nq){
    q = nq;
  }
  PS::F64 getRSearch() const {
    return CUTOFF_LENGTH;
  }
  void copyFromFP(const FPLJ & fp) {
    id = fp.id;
    q = fp.q;
  }
};

実際に力の計算を行うクラスCalcForceLJは、i粒子とj粒子へのポインタと数²、及び結果の格納先へのポインタを受け取る。ガワだけ書くとこんな感じ。

class CalcForceLJ {
public:
  void operator() (const EPLJ * epi, const PS::S32 ni,
                   const EPLJ * epj, const PS::S32 nj,
                   ForceLJ *force) {
  }
};

以上でようやく

tree_lj.calcForceAllAndWriteBack(CalcForceLJ(), lj_system, dinfo);

のコンパイルが通るようになった。

力計算の中身を書く。

まず、粒子を２つ、適当な距離離しておいてみる。

  const int N = 2;
  lj_system.setNumberOfParticleLocal(N);
  lj_system[0].id = 0;
  lj_system[0].p = PS::F64vec(1.0, 0.0, 0.0);
  lj_system[0].q = PS::F64vec(2.5, 5.0, 5.0);
  lj_system[1].id = 1;
  lj_system[1].p = PS::F64vec(-1.0, 0.0, 0.0);
  lj_system[1].q = PS::F64vec(7.5, 5.0, 5.0);

CalcForceLJの中身として、こんなものを書いてみる。

class CalcForceLJ {
public:
  void operator() (const EPLJ * epi, const PS::S32 ni,
                   const EPLJ * epj, const PS::S32 nj,
                   ForceLJ *force) {
    for (PS::S32 i = 0; i < ni; i++) {
      for (PS::S32 j = 0; j < nj; j++) {
        printf("%d %d\n",epi[i].id,epj[j].id);
      }
    }
  }
};

実行するとこうなる。

要するに、

i粒子リストとj粒子リストに同じ粒子が入り得る
作用反作用は考慮されていないらしい

ということがわかる。以上から、

粒子にIDを付与して同じ粒子の計算ははじく
i粒子のみの力を計算する

ということをすれば良さそうである。力の計算と同時に、ポテンシャルエネルギーも計算しておこう。

class CalcForceLJ {
public:
  void operator() (const EPLJ * epi, const PS::S32 ni,
                   const EPLJ * epj, const PS::S32 nj,
                   ForceLJ *force) { 
    const PS::F64 CL2 = CUTOFF_LENGTH*CUTOFF_LENGTH;
    const PS::F64 CL6 = CL2*CL2*CL2;
    const PS::F64 CL12 = CL6*CL6;
    const PS::F64 C0 = - 4.0 * (1.0/CL12 - 1.0/CL6);
    
    for (PS::S32 i = 0; i < ni; i++) {
      force[i].force = 0.0; 
      force[i].potential = 0.0;
      for (PS::S32 j = 0; j < nj; j++) {
        if(epi[i].id == epj[j].id) continue;
        PS::F64vec dq = epj[j].q - epi[i].q;
        PS::F64 r2 = dq * dq;
        PS::F64 r6 = r2*r2*r2;
        PS::F64 r12 = r6 * r6;
        if (r2 > CL2) continue;
        PS::F64 df = (24.0 * r6 - 48.0) / (r6 * r6 * r2);
        force[i].force += dq * df;
        force[i].potential += (4.0 * (1.0 / r12 - 1.0 / r6) + C0)*0.5;
      } 
    } 
  } 
};

ここで、ポテンシャルエネルギーに0.5をかけているのは、「1粒子あたりのポテンシャルエネルギー」にするためである。あとで粒子ごとのポテンシャルエネルギーの総和を取るが、それがそのままポテンシャルエネルギーになるので都合が良い。二体力の場合は後で総和を2で割っても良いが、3体力以上の場合には面倒なことになるので、ポテンシャルエネルギーの計算時に粒子あたりの量に分解しておくと後でいろいろ便利³。

これで、1次のシンプレクティック積分の1ステップはこうかける。

    drift(lj_system, dt);
    tree_lj.calcForceAllAndWriteBack(CalcForceLJ(), lj_system, dinfo);
    kick(lj_system, dt);

力の計算時に1粒子あたりのポテンシャルエネルギーを計算し、それがFPLJのpotentialに書き戻されているため、エネルギーの計算はその総和を求めるだけで良い。

template<class Tpsys>
PS::F64
energy(const Tpsys &system){
  PS::F64 e = 0.0;
  const PS::S32 n = system.getNumberOfParticleLocal();
  for(PS::S32 i = 0; i < n; i++) {
    FPLJ a = system[i];
    e += (a.p*a.p)*0.5;
    e += a.potential;
  }
  return e;
}

以上で全ての計算の準備がととのった。

時間発展

まず、二粒子の正面衝突を計算してみる。メインループはこんな感じにかける。

  const PS::F64 dt = 0.01;
  PS::F64 s_time = 0.0;
  const int LOOP = 1000;
  dinfo.decomposeDomainAll(lj_system);
  for(int i=0;i<LOOP;i++){

    drift(lj_system, dt);
    tree_lj.calcForceAllAndWriteBack(CalcForceLJ(), lj_system, dinfo);
    kick(lj_system, dt);

    std::cout << s_time << " ";
    std::cout << lj_system[0].q.x << " ";
    std::cout << lj_system[1].q.x << " ";
    std::cout << energy(lj_system) << " ";
    std::cout << std::endl;
    lj_system.adjustPositionIntoRootDomain(dinfo);
    s_time += dt;
  }

計算開始前にdinfo.decomposeDomainAllを呼んでおかないと結果がおかしくなるので注意。結果はこんな感じ。

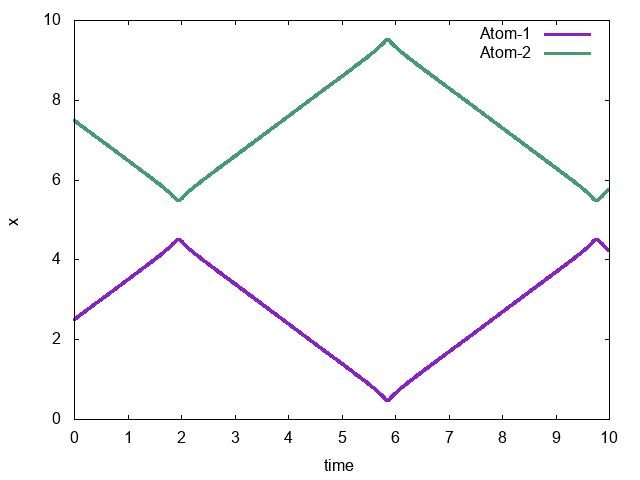
粒子が近づいていき、ある程度近づくと引力により加速し、その後は斥力により反発すして離れていく、というのを繰り返しているのがわかる。

全エネルギーの時間発展はこんな感じ。

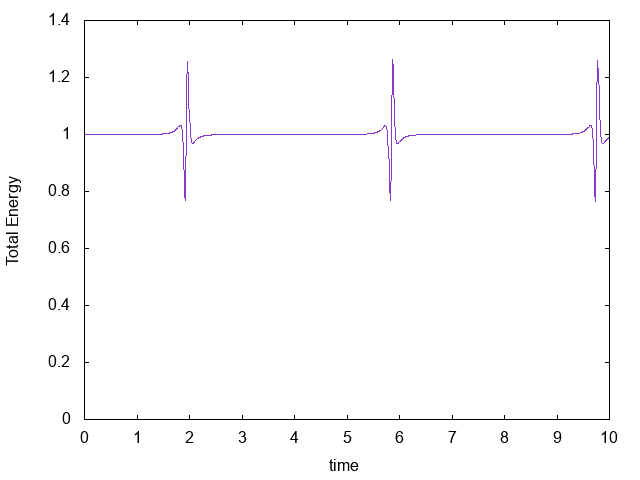
1次の時間積分スキームで、時間刻みも$0.01$と比較的大きいため、わりとぶれている。

というわけで2次の時間積分スキームを使ってみる。

  const PS::F64 dt = 0.01;
  PS::F64 s_time = 0.0;
  const int LOOP = 1000;
  for(int i=0;i<LOOP;i++){

    drift(lj_system, dt*0.5);
    tree_lj.calcForceAllAndWriteBack(CalcForceLJ(), lj_system, dinfo);
    drift(lj_system, dt*0.5);

    std::cout << s_time << " ";
    std::cout << lj_system[0].q.x << " ";
    std::cout << lj_system[1].q.x << " ";
    tree_lj.calcForceAllAndWriteBack(CalcForceLJ(), lj_system, dinfo);
    std::cout << energy(lj_system) << " ";
    std::cout << std::endl;
    lj_system.adjustPositionIntoRootDomain(dinfo);
    s_time += dt;
  }

ここで重要なのは、エネルギーを測定する瞬間のポテンシャルエネルギーが正しく計算されていないといけないこと。具体的にはenergy(lj_system)を呼ぶ直前にtree_lj.calcForceAllAndWriteBackを呼んでやる必要がある(そうしないとエネルギーが2次のスキームの結果を反映しない)⁴。

二次のスキームでも軌道はほとんどかわらないが、エネルギーの保存はかなり改善する。

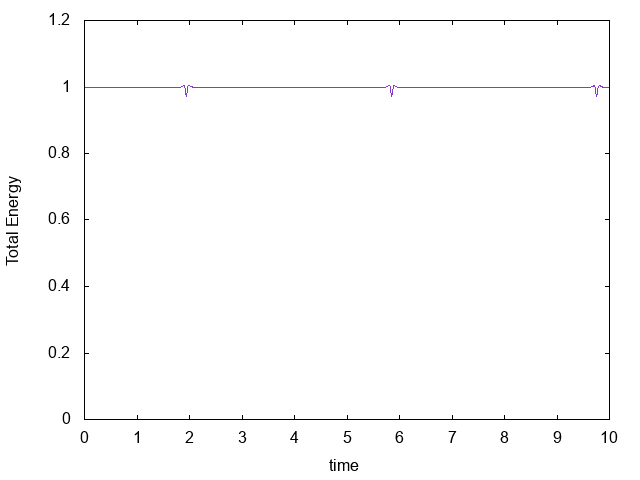
#　まとめ

FDPSを使って相互作用のある粒子系を定義し、二粒子衝突を計算させてみた。短距離相互作用系の相互作用ペアリストをツリーで作ったことがないので、これが正しい使い方なのかも、効率的のかもわからない。後、ざっと見た感じ作用反作用は使えないようだったので使ってないが、もしかしたらサポートする枠組みがあるのかもしれない。

以下のリポジトリのstep4でmake testすれば、コンパイルからpng作成までやってくれるはず。

https://github.com/kaityo256/fdps_sample

その5に続く。

全部publicにするならstructでいいじゃん、という話だが、まぁ個人的な趣味で、メソッドを持つやつはclass、そうでない奴はstructと使い分けてる。 ↩
なんでstd::vector的なものにしなかったんだろう？速度的な問題？ ↩
三体力以上のポテンシャルエネルギーの粒子あたりの量への分解にはいろんな方法があるが、三体力を二体力に分解して、二体力によるポテンシャルを二粒子に等分配する方法が一般的だと思われる。 ↩
この例では力の計算を毎ステップ2回やっているが、実際にはたまにしかエネルギーを計算しないので、観測の直前にcalcForceAllAndWriteBackを呼ぶ、と覚えておけば問題ないと思われる。 ↩

FDPSを使ってみる その4