Tucker分解による画像の低ランク近似
Tucker分解による画像の低ランク近似
はじめに
特異値分解、してますか?>挨拶
今の職場、毎週あるミーティングでみんなが発表するんですが、だいたい「こんなものをSVDしました」という感じなので、僕もSVDしてみたのですが、その続きです。
ソースコードは https://github.com/kaityo256/image_svd においてあります。
はじめにお断りしておきますが、僕はテンソル、というか線形代数全般が苦手です1。なので以下の情報の正確性については保証できません。自分が「あれ?どの足をつぶすんだっけ?」とかごちゃごちゃになるので、その覚書のつもりです。
また、行列$A$の随伴行列(転置して各成分の複素共役をとったもの)を$A^\dagger$で表記することにします。
特異値分解と行列の近似
特異値分解
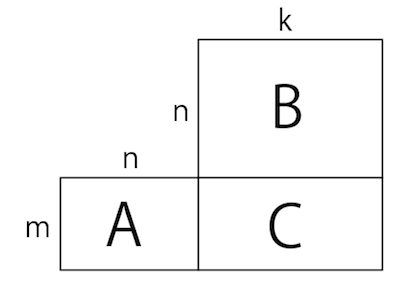
まず、行列の積を考えます。m行n列の行列と、n行k列の行列の積を取ると、m行k列の行列ができます。
\[\begin{aligned} C &= A B \\ C_{ik} &= A_{ij} B_{jk} \end{aligned}\]上の式はアインシュタイン規約を使っています。この時、真ん中にある足がつぶれます。図解するとこんな感じです。
さて、ある行列の情報を圧縮することを考えます。それは、行列の次元を削減することに相当します。まず、例えば$m$行$n$列の行列$X$を、$m$行$n’$列$(n’<n)$として近似することを考えます。その「圧縮機」の役割を果たす$n$行$n’$列の行列$P$があると考えましょう。
$X$に$P$をかけると、列の数が$n$から$n’$に減った$\chi$ができます。図解するまでもありませんが、こんな感じです。
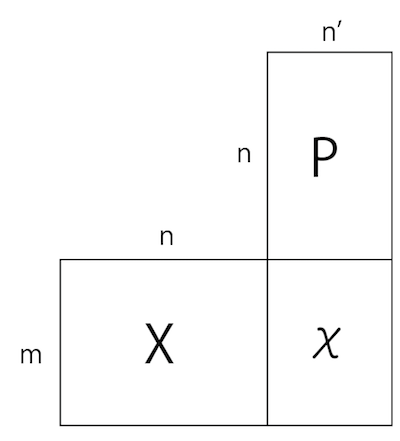
高さはそのままで、幅が狭くなりました。
圧縮された$\chi$から元の$X$に戻すには、$P^\dagger$をかけます。
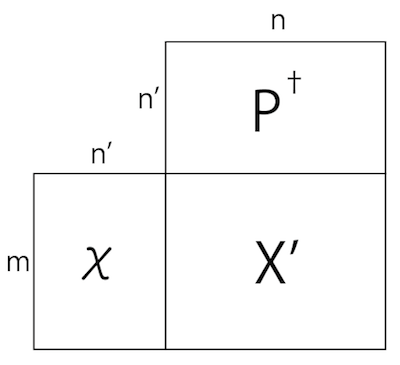
すると、圧縮された行列$\chi$はまた$m$行$n$列の行列になりますが、情報が落ちているために$X$には戻らず、$X$を近似した行列$X’$になります。
要するに$P$は情報圧縮、$P^\dagger$は情報復元の行列で、イメージとしてはドラえもんの道具「ガリバートンネル」のようなものです。ただし、こちらの場合は不可逆ですが・・・
さて、このような情報圧縮/復元行列$P$は、特異値分解(Singular Value Decomposition, SVD)で作ることができます。
SVDは、$m$行$n$列の行列$X$を、
\[X = U \Sigma V^{\dagger}\]という形に分解します。ただし$U$は$m$行$m$列、$V$は$n$行$n$列のユニタリ行列で、$\Sigma$は対角成分しかない$m$行$n$列の行列です。この対角成分を特異値と呼びます。
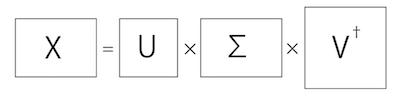
こうしてできた$U$や$V$が情報圧縮機になっています。PythonなどでSVDをすると、特異値の大きさの順番に並べてくれます。この例えば$V^\dagger$の上から$n’$行を取ってできた行列$v^\dagger$が復元機、その随伴行列$v$が圧縮機として使えます。
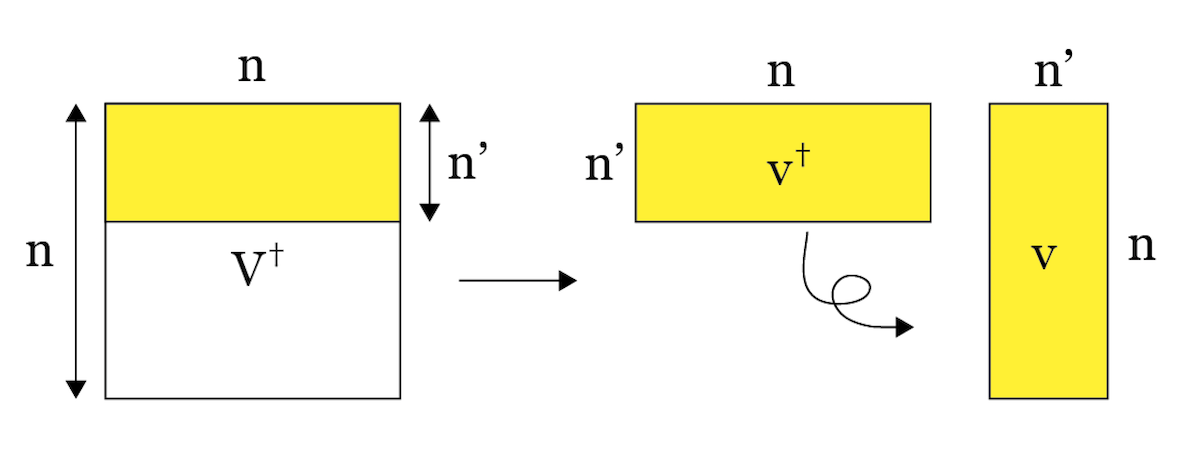
同様に、$U$の左から$m’$列をとったものが圧縮機、その随伴行列が復元機となります。
Tucker分解
上記の例では行列を圧縮しましたが、より一般に高rank(足がいっぱいある)テンソルを圧縮したいことがあります。機械学習なんかでは、データをテンソルだと思って、前処理として圧縮してから学習にかける、といったことが行われているようです。このテンソルの圧縮に使われるのがTucker分解です。
例えば3本の足を持つテンソル$X$を考えます。それぞれの足の次元は$m,n,k$としましょう。これを、より小さな次元$m’,n’,k’$の足を持つテンソル$χ$で近似することを考えます。
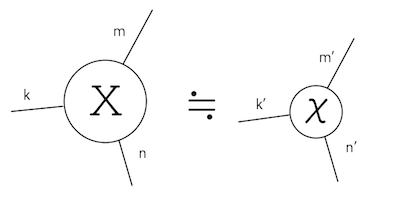
この時、$m$の次元を持つ足を$m’$に潰さなければなりません。これを行列の時と同様にSVDでやります。
まず、潰す足以外の足をまとめます。
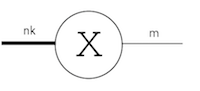
もともと$m,n,k$の3階だったテンソルを$m, n*k$の2階のテンソル、すなわち行列とみなしただけです。するとこれは行列なので、SVDが使えます。
\[X = U \Sigma V^\dagger\]ここで、$V$はユニタリ行列なので、$V V^\dagger = I$、すなわち恒等演算子になります。
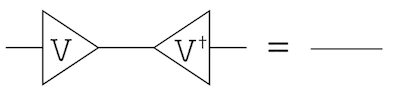
ですが、$V^\dagger$の上位$m’$列をとった行列を$v^\dagger$とすると、$v$は$m$から$m’$への圧縮機に、$v^\dagger$は$m’$から$m$への復元機になります。
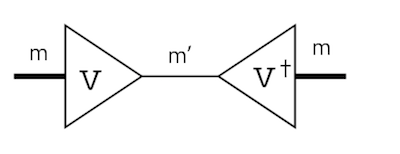
この圧縮機をそれぞれの足について作ってからかけてやると、元々のテンソル$X$を縮小したテンソル$\chi$が得られます。
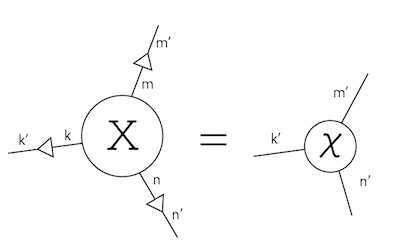
こうして得られた縮小されたテンソルをコアテンソル(core tensor)と呼びます。コアテンソルから元のテンソルの復元には、それぞれの足に復元機をかけてやればよいことになります。
こういう分解をHigher Order SVD, HOSVDと言うみたいです。
画像圧縮への応用
ではSVDを使って画像を圧縮してみましょう。
二次元の画像データは、x座標、y座標、色を指定すると値が決まるため、3階のテンソルとみなすことができます。幅$w$、高さ$h$ならば、それぞれの足の次元(太さ)は$w,h,c$です。ただしcはcolorで次元は3です。データを素直に読み込むと、高さ、幅、色の順番になるので、これをX[y,x,c]と表現することにします。
これをSVDを使って圧縮する際、もっとも簡単には前回やったようにRGBプレーンそれぞれに対してSVDをかけてしまうことです。
img = Image.open(filename)
w = img.width
h = img.height
X = np.asarray(img)
r = perform_svd(X[:,:,0],rank).reshape(w*h)
g = perform_svd(X[:,:,1],rank).reshape(w*h)
b = perform_svd(X[:,:,2],rank).reshape(w*h)
B = np.asarray([r,g,b]).transpose(1,0).reshape(h,w,3)
PILのImageでファイルをオープンし、それをnumpy.asarrayにつっこむと、(高さ、幅、色)の3階のテンソルXになります。例えばX[:, :, 0]とすれば赤のイメージが取れるので、それをSVDにより近似します。同様に緑、青の近似画像を作ってから、適当にtranspose、reshapeすると元の画像に戻せます。2
次に、HOSVDを使ってみましょう。画像を(h,w,c)のテンソルXにするところまでは同じです。まず幅や高さをつぶすための行列を得るために、高さと色の足をまとめた行列X1と、幅と色の足をまとめた行列X2を作っておきましょう。
X1 = X.transpose(0,2,1).reshape(h*3,w)
X2 = X.transpose(1,2,0).reshape(w*3,h)
足の順番を(h,w,c)から、それぞれ(hc,w)と(wc,h)の行列にしているだけです。これをそれぞれSVDします。
U,s,A1 = linalg.svd(X1)
U,s,A2 = linalg.svd(X2)
得られたA1、A2の上位$r$列を取ることで復元機a1、a2が作れます。
a1 = A1[:r2, :]
a2 = A2[:r2, :]
今回はこいつらは実行列なので転置すればダガーがとれます。
あとは、a1.Tをかけて潰してから$a1$をかけて復元するわけですが、面倒なので先に「圧縮/復元」を一度にやる行列(プロジェクタ)を作ってしまいます。
pa1 = a1.T.dot(a1)
pa2 = a2.T.dot(a2)
こうしてできたプロジェクタを適切な足とtensordotすれば近似されたテンソルを得ることができます。
X2 = np.tensordot(X,pa1,(1,0))
X3 = np.tensordot(X2,pa2,(0,0))
X4 = X3.transpose(2,1,0)
ここでは、x座標の足とy座標の足だけつぶして、色の足はつぶしていません。以上のコードは、
https://github.com/kaityo256/image_svd
の、color_tuckerに実装しています。
比較
RGBプレーンそれぞれを行列だと思ってSVDをかけるのと、3本の足を2本にまとめてSVDをかけるのを二回やる(HOSVD)を比較してみます。まず、それぞれどれだけ情報が圧縮されたかを調べます。$L_1\times L_2$のカラー画像を考えましょう。これを$r$までのランクで近似します。
RGBプレーンそれぞれをSVDする場合は、各色の画像が$L_1 \times L_2$の行列になっており、それが$L_1 r$と$L_2 r$、r個の特異値に圧縮されます。それが3色あるので、$3L_1 L_2$の情報が$3r(L_1 + L_2 + r)$に圧縮されます。$L_1, L_2 \gg r$とすると$3r(L_1 + L_2)$です。
HOSVDの方は、$L_1 \times L_2 \times 3$のテンソルが、$r \times r\times 3$のコアテンソルと、$L_1\times r$、$L_2 \times r$の行列に圧縮されるため、圧縮後のデータ量は$r(L_1+L_2+3r)\sim r(L_1 + L_2)$となります。となります。従って、RGBプレーンで$r$までのランクで近似した場合と同じ情報量に圧縮するためには、HOSVDでは$3r$まで取ればよいことになります。
以下、適当な画像での比較です。
元画像

RGBプレーンそれぞれ上位10個のランクを残したもの

HOSVDで、x座標y座標のプロジェクタとして上位30個のこしたもの。

同じ情報量を残しているはずですが、HOSVDの方がいいみたいですね。
まとめ
画像データを高さ、幅、色の3つの足をもつ3階テンソルだと思って、Tucker分解し、近似画像を作ってみました。同じ情報量で比較した場合は、RGBプレーンそれぞれをSVDするよりも、足をまとめてSVDする、HOSVDの方が良いみたいですね。また、今回はそれぞれの足で一回だけSVDをしましたが、これを繰り返し行うことで近似精度を上げるhigher order orthogonal iteration (HOOI)というのもあるみたいです。
 A Robot’s Sigh
A Robot’s Sigh