最小二乗法の幾何学的な意味
はじめに
$N$個のデータ点を$M$個のパラメーを用いて最小二乗法でフィッティングしようとする時、これは$N$次元空間のデータ点から、$M$次元部分空間への正射影を求める問題と等価になります。ですが、$N$次元空間とか$M$次元部分空間とか言われても普通は想像できません。また、元々フィッティングしようとしていたデータの住む空間とは異なる空間での話になるのも混乱を助長します。
以下では簡単な系で「なるほど、たしかに最小二乗法は射影だな」と思えるような説明を試みます。
最小二乗法
まずは最小二乗法を定式化しておきましょう。簡単のため、データはスカラーであるとします。何か入力値$x$があるとき、その出力$y$を予想する関数$y = f(x)$を推定するのが目的です。
$N$個入力点$x_1, x_2, \cdots, x_N$に対して、観測値$y_1, y_2, \cdots, y_N$が与えられているとします。これを$M$個のパラメータ$\theta_1, \theta_2, \cdots, \theta_M$を持つ関数$f(x; \vec{\theta})$で近似することにします。ただし$\vec{\theta}$はパラメータをまとめて書いたものです。
| 例えば、入力値が$x_i$だったとして、推定値は$\tilde{y}_i = f(x_i; \vec{\theta})$となります。正解データは$y_i$ですから、誤差は$ | y_i - \tilde{y}_i | $です。これが$N$点あるのですから、これらの二乗和$E$を近似の誤差としましょう。 |
この$E$を最小化するようにパラメータを決めましょう、というのが最小二乗法です。
例を挙げましょう。パラメータを一つだけとし、$\theta_1 = a$とします。推定関数を$y = ax$としましょう。入力$x_i$に対する推定値は$\tilde{y}_i = a x_i$なので、誤差は
\[\begin{aligned} E &= \sum_i (y_i - a x_i)^2\\ &= a^2 \sum_i x_i^2 - 2 a \sum_i x_i y_i + \sum_i y_i^2 \end{aligned}\]となります。あとの計算のために二乗を展開しておきました。これを最小にする$a$を求めるため、$a$で微分します。
\[\begin{aligned} \frac{\partial E}{\partial a} &= 2a \sum_i x_i^2 - 2 \sum_i x_i y_i\\ &= 0 \end{aligned}\]ここから、
\[a = \frac{ \sum_i x_i y_i}{\sum_i x_i^2}\]と求められます。ここまでは「誤差を微分してゼロとなるようなパラメータが最小値を与えるよね」という解析学的な扱いでしたが、この幾何学的な意味を考えよう、というのが本稿の目的です。
幾何学的な解釈
もう一度誤差を見てみましょう。
\[E = \sum_i (y_i - \tilde{y}_i)^2\]ここで、$\vec{y} = (y_1, y_2, \cdots, y_N)$、$\vec{\tilde{y}} = (\tilde{y}_1, \tilde{y}_2, \cdots, \tilde{y}_N)$というベクトルを定義すると
\[E = |\vec{y} - \vec{\tilde{y}}|^2\]と書き直せます。これは2つの$N$次元ベクトルの距離です。これを最小化しようと言うのですから、最小二乗法は「与えられたベクトル$\vec{y}$に対して、なるべく$\vec{\tilde{y}}$を近づけるようにパラメータを選ぶ作業」となります。いま、パラメータが$M$個であるとするなら、パラメータをいろいろ変えてみると、$\vec{\tilde{y}}$は($N$次元ベクトルだけれど)$M$次元空間を動くことになります。この辺がわかりにくいので、具体例を見てみましょう。
パラメータ1つの場合
データ点$N=2$、パラメータ数$M=1$の場合を考えます。いま、データ点として
\[\begin{pmatrix} x_i \\ y_i \end{pmatrix} = \begin{pmatrix} 1 \\ 1.1 \end{pmatrix}, \begin{pmatrix} 2 \\ 1.8 \end{pmatrix}\]の2点が与えられているとしましょう($N=2$)。これを
\[y = a x\]という一つのパラメータを持つ関数でフィッティングします($M=1$)。データ点のベクトルは
\[\vec{y} \equiv \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \begin{pmatrix} 1.1 \\ 1.8 \end{pmatrix}\]という二次元ベクトルになります。同様に、データ点の推定ベクトルは
\[\vec{\tilde{y}} \equiv \begin{pmatrix} \tilde{y}_1 \\ \tilde{y}_2 \end{pmatrix} = \begin{pmatrix} a x_1 \\ a x_2 \end{pmatrix} = \begin{pmatrix} a \\ 2a \end{pmatrix}\]となります。このベクトル$\vec{\tilde{y}}$は2次元ベクトルですが、パラメータ$a$を色々かえると、直線上を動きます。したがって、パラメータ$a$をいろいろ変えた時の$\vec{\tilde{y}}$の軌跡の集合は直線になります。
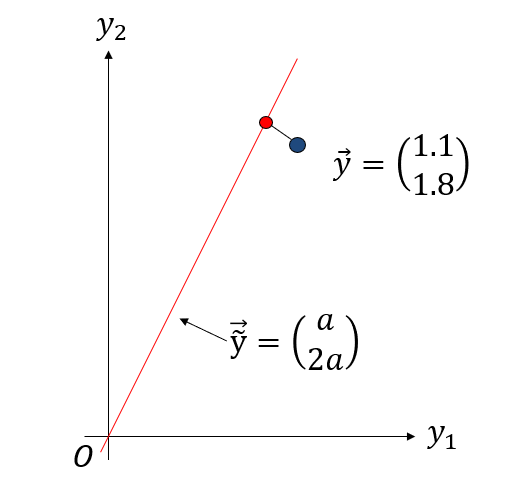
我々の目的はデータ点ベクトル$\vec{y}$と、推定ベクトル$\vec{\tilde{y}}$をなるべく近づけることですから、幾何学的にはデータ点ベクトルから、推定ベクトル$\vec{\tilde{y}}$が描く直線に垂線を下ろし、その足が求める最良推定点であり、その点を与えるパラメータがフィッティング結果ということになります。
パラメータ2つの場合
データ点$N=3$、パラメータ数$M=2$の場合を考えます。いま、データ点として
\[\begin{pmatrix} x_1 \\ y_1 \end{pmatrix} , \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} , \begin{pmatrix} x_3 \\ y_3 \end{pmatrix}\]の3点が与えられているとしましょう($N=2$)。これを
\[y = a x + b\]という2つのパラメータを持つ関数でフィッティングします($M=2$)。データ点のベクトルは
\[\vec{y} \equiv \begin{pmatrix} y_1 \\ y_2 \\ y_3 \end{pmatrix}\]という3次元ベクトルになります。同様に、データ点の推定ベクトルは
\[\vec{\tilde{y}} \equiv \begin{pmatrix} \tilde{y}_1 \\ \tilde{y}_2 \\ \tilde{y}_3 \end{pmatrix} = \begin{pmatrix} a x_1 + b \\ a x_2 + b \\ a x_3 + b \end{pmatrix}\]となります。このベクトル$\vec{\tilde{y}}$は3次元ベクトルですが、パラメータ$a,b$を色々かえると、平面上を動きます。したがって、パラメータをいろいろ変えた時の$\vec{\tilde{y}}$の軌跡の集合は平面になります。
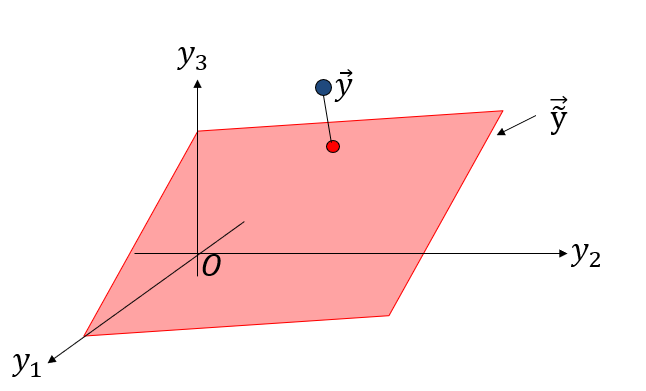
この平面上の点で、最もデータ点ベクトル$\vec{y}$に近いものを探したいのですから、データ点ベクトルからこの平面に垂線を下ろし、その足が求める最良推定点であり、またその点を与えるパラメータがフィッティング結果となります。
まとめ
最小二乗法はデータ点ベクトル$\vec{y}$と、その推定ベクトル$\vec{\tilde{y}}$をなるべく近づけようとする手法であり、データ点が$(x, y)$という二次元の住人であっても、データ数が$N$点あったらデータ点ベクトル$\vec{y}$は$N$次元空間の住人になるところがちょっとわかりにくいポイントです。
それさえわかってしまえば、「$N$個のデータを$M$個のパラメータでフィッティングする」という問題は、「$N$次元空間中にあるベクトルから、$M$次元部分空間に正射影する」という問題になることはわかりやすいのかな、と思います。例えば$N=2, M=1$なら、2次元空間上の点から直線への垂線に、$N=3, M=2$なら、3次元空間上の点から平面への垂線となります。
PRMLの3.1.2節に最小二乗法の幾何学的な意味の解説がありましたが、そのままではちょっとわかりにくいかなと思って説明を書いてみました。参考になれば幸いです。
 A Robot’s Sigh
A Robot’s Sigh