MDループのソフトウェアパイプライニング:ステップ・バイ・ステップ
MDループのソフトウェアパイプライニング:ステップ・バイ・ステップ
はじめに
分子動力学法(Molecular Dynamics method, MD)で有効なチューニング技法の一つにソフトウェアパイプライニング(Software pipelining, SWP)というものがある。通常、SWPは依存関係のある命令のレイテンシを隠蔽するのに使われるが、MDにおいてはサイクルあたりの命令実行数(Instructions per cycle, IPC)の向上が目的となる。
率直に言って、手間がそれなりにかかるわりに、「ものすごく早くなる」という技法でもないため、万人におすすめできる方法ではない。
筆者はちょっと前にSWPをやりまくったので、今ならMDのループを機械的にSWPできる。しかし、あと半年もすれば僕もSWPのやりかたを忘れてしまうだろう。それはあまりに悲しい。この手法を忘れる前にここに残しておく。
コードはここにおいておく。
https://github.com/kaityo256/swp_step
ソフトウェアパイプライニングとは
ソフトウェアパイプライニング(以下SWP)とは、ループ内に依存関係がある命令がある場合に、そのレイテンシを隠蔽する技法である。Wikipediaにも例があるが、ここでも簡単に説明してみよう。
以下のようなループ構造を考える。
const int N = 10000;
double a[N], b[N], c[N];
for (int i=0;i<N;i++){
b[i] = f(a[i]); // (1)
c[i] = g(b[i]); // (2)
}
ここで、’f’や’g’は何かの関数である。b[i]'の計算が終わるまでc[i]’の計算ができないため、(1)が終わるまで(2)の実行を開始することができない。
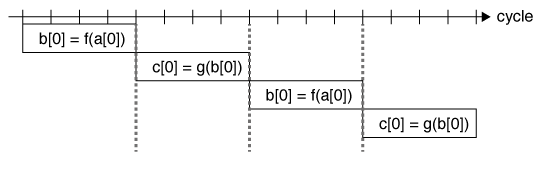
しかし、この計算はiごとに独立に実行できる。ループを二倍展開してみよう。
const int N = 10000;
double a[N], b[N], c[N];
for (int i=0;i<N/2;i+=2){
b[i*2] = f(a[i*2]); (1)
b[i*2+1] = f(a[i*2+1]); (2)
c[i*2] = f(b[i*2]); (3)
c[i*2+1] = f(b[i*2+1]); (4)
}
b[i*2]とb[i*2+1]の計算は独立に実行できるため、(2)は(1)の実行を終わるまで待つことなく実行に入ることができる。(3)と(4)も同様である。もし、それぞれの演算のレイテンシが4サイクルであった場合、4倍にアンロールすればレイテンシを完全に隠蔽することができる。
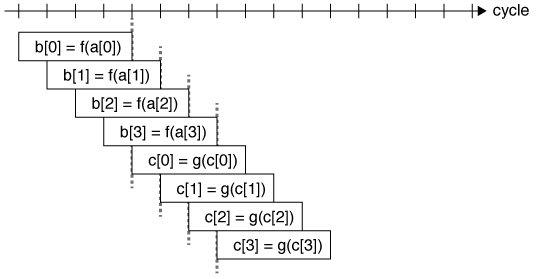
こうして、ループをアンロールすることで、独立に実行できる命令を増やすことで、「前の結果待ち」の時間を減らすことができる。これが一般的なソフトウェアパイプライニングの目的となる。
IPC向上のためのSWP
SWPは演算機のパイプラインの効率をにらんだ最適化であったが、ここではIPC向上のために用いる。最近の石はほとんどの場合スーパースカラを採用しており、サイクルあたり複数の命令を実行できる。例えば、Load/Storeを2命令、浮動小数点命令を2命令、同時に4命令を発行できたりする。このスーパースカラの効率をにらんだ最適化を考える。
MDの力の計算を行うには
- 粒子の座標をloadする
- 距離を計算する
- 力を計算する
- 更新された運動量をstoreする
という処理を繰り返す。
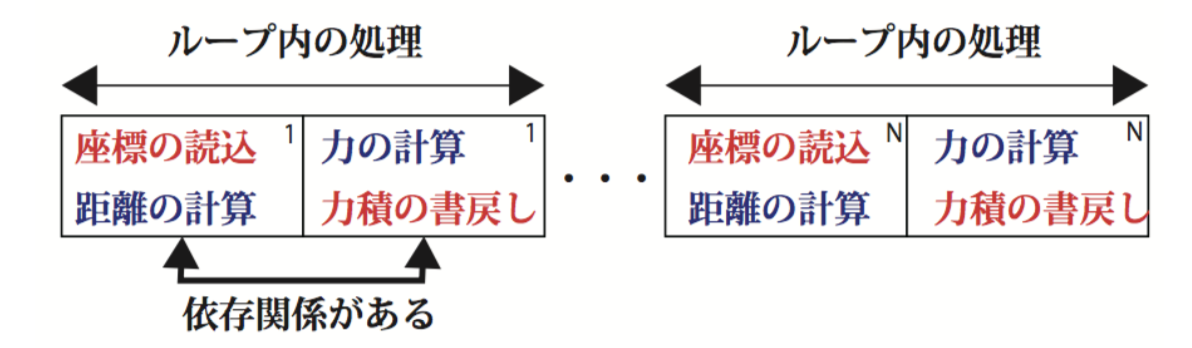
この図だと座標の読み込みと距離の計算が同時にできるように見えるが、実際には依存関係があるのでシリアルな処理となる。
さて、このループを「半個ずらし」することを考える1。つまり、「一つ前のペアの力の計算と力積の書き戻しをやっている間に、次のペアの座標の読み込みと距離の計算」をやる。こんな感じ。
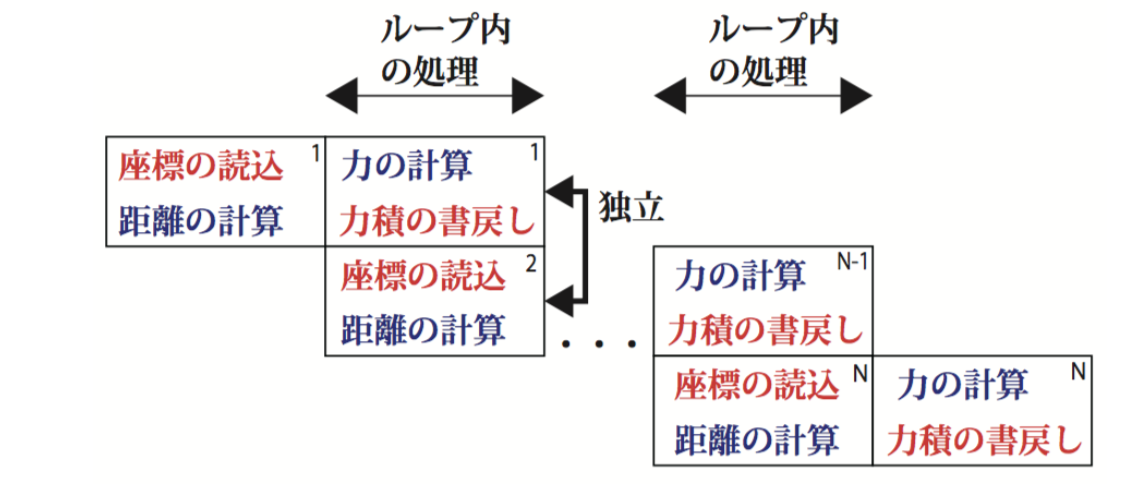
青字で書いたものが計算、赤字で書いたものがメモリアクセスである。相変わらず「箱の中」には依存関係があるが、「箱を縦に積んだ物」は依存関係がないため、同時に命令を発行できる。これにより、IPCを稼ごう、というのがMD向けのSWPである。
実際のコード
さて、概念はわかったとはいえ、実際にどうすればよいかはわからないと思う。なのでステップ・バイ・ステップでSWPをやってみよう。
実行環境は以下の通り。
- Intel(R) Xeon(R) Gold 6148 CPU @ 2.40GHz
- g++ (GCC) 4.8.5 20150623 (Red Hat 4.8.5-16)
Step 0:元のコード
最適化のターゲットとなるコードはこんな感じである。
void
force_sorted(void) {
const int pn = particle_number;
for (int i = 0; i < pn; i++) {
const double qix = q[i][X];
const double qiy = q[i][Y];
const double qiz = q[i][Z];
const int np = number_of_partners[i];
double pfx = 0;
double pfy = 0;
double pfz = 0;
const int kp = pointer[i];
for (int k = 0; k < np; k++) {
const int j = sorted_list[kp + k];
double dx = q[j][X] - qix;
double dy = q[j][Y] - qiy;
double dz = q[j][Z] - qiz;
double r2 = (dx * dx + dy * dy + dz * dz);
double r6 = r2 * r2 * r2;
double df = ((24.0 * r6 - 48.0) / (r6 * r6 * r2)) * dt;
if (r2 > CL2) df = 0.0;
pfx += df * dx;
pfy += df * dy;
pfz += df * dz;
p[j][X] -= df * dx;
p[j][Y] -= df * dy;
p[j][Z] -= df * dz;
}
p[i][X] += pfx;
p[i][Y] += pfy;
p[i][Z] += pfz;
}
}
外側のループがi粒子について、内側のループがj粒子についてのループになっている。i粒子と相互作用する粒子番号がsorted_listに入っているので、ループカウンタはkで回るが、そこからjのインデックスを得ている。
まず、これをリファレンスとし、ある初期条件を与えたとき、更新された運動量を標準出力に吐くようにしよう。
$ ./a.out > orig.txt
A pair-file is found. I use it.
Number of pairs: 7839886
Number of pairs: 7839886
N=119164, sorted 5766 [ms]
以下、何か修正するたびに結果を出力し、このorig.txtとdiffを取ることでデバッグしていく。
Step 1: ループに切れ目をいれる
まずは、半個ずらしするところに切れ目をいれよう。また、ループの半個ずらしは「ループが最低一度はまわる」ということを前提としているため、ループ回転数が0の場合は除外しなければならない。
void
force_sorted_swp1(void) {
const int pn = particle_number;
for (int i = 0; i < pn; i++) {
const double qix = q[i][X];
const double qiy = q[i][Y];
const double qiz = q[i][Z];
const int np = number_of_partners[i];
double pfx = 0;
double pfy = 0;
double pfz = 0;
const int kp = pointer[i];
if (np==0) continue; // 相互作用粒子ゼロなら飛ばす
for (int k = 0; k < np; k++) {
// ------- 8< ---------
const int j = sorted_list[kp + k];
double dx = q[j][X] - qix;
double dy = q[j][Y] - qiy;
double dz = q[j][Z] - qiz;
// ------- 8< ---------
double r2 = (dx * dx + dy * dy + dz * dz);
double r6 = r2 * r2 * r2;
double df = ((24.0 * r6 - 48.0) / (r6 * r6 * r2)) * dt;
if (r2 > CL2) df = 0.0;
pfx += df * dx;
pfy += df * dy;
pfz += df * dz;
p[j][X] -= df * dx;
p[j][Y] -= df * dy;
p[j][Z] -= df * dz;
}
p[i][X] += pfx;
p[i][Y] += pfy;
p[i][Z] += pfz;
}
}
違いは、
if (np==0) continue; // 相互作用粒子ゼロなら飛ばす
が入ったのと、「切り取り線」
// ------- 8< ---------
が二箇所に入っただけである。当然、結果は不変のはずだが、チェックしておいた方がよい。
$ ./a.out > test.txt
A pair-file is found. I use it.
Number of pairs: 7839886
N=119164, sorted_swp1 5847 [ms]
$ diff test.txt orig.txt
$
Step 2:半個ずらし
さて、いよいよループを半個ずらししよう。
内側のループが二つの領域に分かれている。そのうち、前半部分をループの前に、後半部分をループの外に出し、ループの中身を入れ替える。つまり、
for (int k = 0; k < np; k++) {
A(k);
B(k);
}
となっているのを、
A(0)
for (int k = 1; k < np; k++) {
B(k);
A(k);
}
B(np-1);
とする。この時、ループの外に出た変数を、ループの内側で上書きしないように気をつけること。具体的には、jやdxなどからintやdoubleの宣言を外す。またconst int jとなっていたのはint jに修正する。
こんな感じになる。
void
force_sorted_swp2(void) {
const int pn = particle_number;
for (int i = 0; i < pn; i++) {
const double qix = q[i][X];
const double qiy = q[i][Y];
const double qiz = q[i][Z];
const int np = number_of_partners[i];
double pfx = 0;
double pfy = 0;
double pfz = 0;
const int kp = pointer[i];
if (np==0) continue; // 相互作用粒子ゼロなら飛ばす
int j = sorted_list[kp];
double dx = q[j][X] - qix;
double dy = q[j][Y] - qiy;
double dz = q[j][Z] - qiz;
for (int k = 1; k < np; k++) {
// ------- 8< ---------
double r2 = (dx * dx + dy * dy + dz * dz);
double r6 = r2 * r2 * r2;
double df = ((24.0 * r6 - 48.0) / (r6 * r6 * r2)) * dt;
if (r2 > CL2) df = 0.0;
pfx += df * dx;
pfy += df * dy;
pfz += df * dz;
p[j][X] -= df * dx;
p[j][Y] -= df * dy;
p[j][Z] -= df * dz;
// ------- 8< ---------
j = sorted_list[kp + k];
dx = q[j][X] - qix;
dy = q[j][Y] - qiy;
dz = q[j][Z] - qiz;
}
double r2 = (dx * dx + dy * dy + dz * dz);
double r6 = r2 * r2 * r2;
double df = ((24.0 * r6 - 48.0) / (r6 * r6 * r2)) * dt;
if (r2 > CL2) df = 0.0;
pfx += df * dx;
pfy += df * dy;
pfz += df * dz;
p[j][X] -= df * dx;
p[j][Y] -= df * dy;
p[j][Z] -= df * dz;
p[i][X] += pfx;
p[i][Y] += pfy;
p[i][Z] += pfz;
}
}
繰り返しになるが、最内ループの前半部分が前に、後半部分が後ろにはみ出した上で、ループ内が入れ替わったのがわかる。これは純粋にループを半個ずらししただけで、論理的には変更前と等価なループであるはずであるが、ここで一番バグが入りやすいのでちゃんとチェックしておこう。
$ ./a.out > test.txt
A pair-file is found. I use it.
Number of pairs: 7839886
N=119164, sorted_swp2 5576 [ms]
$ diff test.txt orig.txt
$
printfとdiffはデバッグの基本である。
Step 3: 命令の入れ替え
さて、現状でループの中身はこうなっている。
// k番目のペアとの力の計算
// ← ここに飛ばす
// ------- 8< ---------
double r2 = (dx * dx + dy * dy + dz * dz);
double r6 = r2 * r2 * r2;
double df = ((24.0 * r6 - 48.0) / (r6 * r6 * r2)) * dt;
if (r2 > CL2) df = 0.0;
pfx += df * dx;
pfy += df * dy;
pfz += df * dz;
// k番目のペアのj粒子の運動量書き戻し
p[j][X] -= df * dx;
p[j][Y] -= df * dy;
p[j][Z] -= df * dz;
// ------- 8< ---------
// k+1番目の座標の読み込みと相対ベクトルの計算
j = sorted_list[kp + k]; // ← こいつを前半に飛ばす
dx = q[j][X] - qix;
dy = q[j][Y] - qiy;
dz = q[j][Z] - qiz;
我々はk番目の後半処理とk+1番目の前半処理を重ねたいので、明示的にそうするため、ループの後半部分を前半に飛ばす。
まず
j = sorted_list[kp + k]; // ← こいつを前半に飛ばす
この行を前に飛ばそう。ただし、そのまま飛ばしてしまうと、同じ変数jを上書きしてしまう。そこで、一度テンポラリ変数j2に受けて、後で代入しよう。こんな感じになる。
int j2 = sorted_list[kp + k]; //← 飛んできた行
// ------- 8< ---------
double r2 = (dx * dx + dy * dy + dz * dz);
double r6 = r2 * r2 * r2;
double df = ((24.0 * r6 - 48.0) / (r6 * r6 * r2)) * dt;
if (r2 > CL2) df = 0.0;
pfx += df * dx;
pfy += df * dy;
pfz += df * dz;
p[j][X] -= df * dx;
p[j][Y] -= df * dy;
p[j][Z] -= df * dz;
// ------- 8< ---------
//j = sorted_list[kp + k]; //飛び先で計算した結果を復帰
j = j2;
dx = q[j][X] - qix;
dy = q[j][Y] - qiy;
dz = q[j][Z] - qiz;
これにより、k番目のループの計算と、k+1番目のj粒子のインデックスの読み込みが重なった。これは独立に実行できるはずなので、IPCが上がるはずである。その代わり、代入命令が増えることに注意。
ここでもちゃんとdiffを取っておこう。
$ ./a.out > test.txt
A pair-file is found. I use it.
Number of pairs: 7839886
N=119164, sorted_swp3 5218 [ms]
$ diff test.txt orig.txt
$
大事なことなのでしつこく書く。高速化チューニングでバグを入れたら本末転倒なので。また、この時点でリファレンスコードよりも少しだけ速度が早くなったことがわかるかと思う。
Step 4: SWP完成
同様に、dx, dy, dzの計算も「前」に飛ばすことができる。その際、一次変数 dx2, dy2, dz2を使うのは前回と同様。力の計算はこうなった。
void
force_sorted_swp4(void) {
const int pn = particle_number;
for (int i = 0; i < pn; i++) {
const double qix = q[i][X];
const double qiy = q[i][Y];
const double qiz = q[i][Z];
const int np = number_of_partners[i];
double pfx = 0;
double pfy = 0;
double pfz = 0;
const int kp = pointer[i];
if (np==0) continue; // 相互作用粒子ゼロなら飛ばす
int j = sorted_list[kp];
double dx = q[j][X] - qix;
double dy = q[j][Y] - qiy;
double dz = q[j][Z] - qiz;
for (int k = 1; k < np; k++) {
int j2 = sorted_list[kp + k];
double dx2 = q[j2][X] - qix;
double dy2 = q[j2][Y] - qiy;
double dz2 = q[j2][Z] - qiz;
// ------- 8< ---------
double r2 = (dx * dx + dy * dy + dz * dz);
double r6 = r2 * r2 * r2;
double df = ((24.0 * r6 - 48.0) / (r6 * r6 * r2)) * dt;
if (r2 > CL2) df = 0.0;
pfx += df * dx;
pfy += df * dy;
pfz += df * dz;
p[j][X] -= df * dx;
p[j][Y] -= df * dy;
p[j][Z] -= df * dz;
// ------- 8< ---------
//j = sorted_list[kp + k];
//dx = q[j][X] - qix;
//dy = q[j][Y] - qiy;
//dz = q[j][Z] - qiz;
j = j2;
dx = dx2;
dy = dy2;
dz = dz2;
}
double r2 = (dx * dx + dy * dy + dz * dz);
double r6 = r2 * r2 * r2;
double df = ((24.0 * r6 - 48.0) / (r6 * r6 * r2)) * dt;
if (r2 > CL2) df = 0.0;
pfx += df * dx;
pfy += df * dy;
pfz += df * dz;
p[j][X] -= df * dx;
p[j][Y] -= df * dy;
p[j][Z] -= df * dz;
p[i][X] += pfx;
p[i][Y] += pfy;
p[i][Z] += pfz;
}
}
若干長くなった気がするが、それはコメントアウトされた行のせいもあるので、それらを消せばさほど長くはない・・・と思う。
何はともあれ、これでSWPは完成である。早速実行してみよう。
$ ./a.out > test.txt
A pair-file is found. I use it.
Number of pairs: 7839886
N=119164, sorted_swp4 4830 [ms]
$ diff test.txt orig.txt
$
無事に 5766 [ms] → 4830 [ms]に高速化された。
これがIPC向上によるものであることはperfを取るとわかる。
- SWP前
18,190,658,852 cycles # 3.100 GHz
28,717,014,184 instructions # 1.58 insn per cycle
- SWP後
15,270,075,565 cycles # 3.100 GHz
32,622,329,679 instructions # 2.14 insn per cycle
命令数が28.7G個から32.6G個に増えたかわりに、サイクル数が18.2G cycleから15.3G cycleに減っていることがわかる。命令数の増加割合よりも、IPCの増加割合(1.58→2.14)の方が大きいため、全体として加速する、という仕組みになっている。
まとめ
MDにおけるSWPのやり方をまとめた。そもそもこういう細かいチューニング技法はあまり文書化されない傾向にあるし、されたとしても概念と改変結果だけ示されることがほとんどであろう。
実際には
- ループに切れ込みをいれる
- ループを半個ずらしする
- 命令を少しずつ「前」に飛ばす
ということをやって、一つ一つの過程でバグを入れていないか確認をしている。一度にSWPしようとすると間違いなくデバッグに手間取るので、ステップ・バイ・ステップにやるのがコツである。
冒頭にも書いたが、これは万人におすすめできる手法ではない。しかし、この最適化だけで20%近い速度ゲインがあるし、SIMD化とも組み合わせられるため、頭の片隅においておくと良いことがあるかもしれない。
願わくば、数年後、この記事が世界一を目指すような誰かに発掘され、何かの役に立ちますように。
参考
-
なんとなくイースの半キャラずらしを思い出す(←おっさん)。 ↩
 A Robot’s Sigh
A Robot’s Sigh