分子動力学法における熱浴の保存量
分子動力学法における熱浴の保存量
はじめに
分子動力学法において、Nose-Hoover法は温度制御に広く使われている。Nose-Hoover法は能勢の拡張ハミルトニアンの方法にもとづいており、いわゆる「能勢のハミルトニアン」に起因する保存量(第一積分)がある。しかし、Nose-Hoover法の多変数版であるKinetic-Moments法やNose-Hoover-Chain法には同様な議論が無く1、能勢のハミルトニアンに起因する保存量は存在しない。しかし、拡張ハミルトニアンを忘れ、純粋に運動方程式のみを考慮することで、Nose-Hoover法と同様な保存量を構築することができる。
本稿では、Nose-Hoover法、Kinetic-Moments法、Nose-Hoover-Chain法における保存量の構築について述べる。
保存量の構築
Nose-Hoover法
以下、自然ハミルトニアン
\[H = \frac{p^2}{2} + V(q)\]を考える。質量は1としている。簡単のため一自由度系を考慮するが、多自由度系への適用は易しい。Nose-Hoover法の運動方程式は以下で与えられる。
\[\begin{aligned} \dot{p} &= - \frac{\partial H}{\partial q} - \frac{\zeta p}{Q}\\ \dot{q} &= \frac{\partial H}{\partial p}\\ \dot{\zeta} &= p^2 - \frac{1}{\beta} \end{aligned}\]この系は、以下の拡張されたハミルトニアン$H_\mathrm{ex}$について、逆温度$\beta$カノニカル分布が定常分布となる。
\[H_\mathrm{ex} = H + \frac{\zeta^2}{2Q}\]さて、この拡張されたハミルトニアン$H_\mathrm{ex}$の時間微分を考える。
\[\dot{H}_\mathrm{ex} = \frac{\partial H}{\partial p}\dot{p} +\frac{\partial H}{\partial q}\dot{q} + \frac{\zeta \dot{\zeta}}{Q}\]上記の式に運動方程式を代入して整理すると、以下を得る。
\[\dot{H}_\mathrm{ex} = - \frac{\zeta}{\beta Q}\]さらに拡張されたハミルトニアン$H_\mathrm{c} = H_\mathrm{ex} + \eta$を考える。ここで、
\[\dot{\eta} = - \dot{H}_\mathrm{ex} = \frac{\zeta}{\beta Q}\]とすれば、当然ながら
\[\dot{H}_{\mathrm{c}} = 0\]であるから、$H_{\mathrm{c}}$が保存量となる。
新たに加えた自由度$\eta$を含めると、以下の運動方程式を得る。
\[\begin{aligned} \dot{p} &= - \frac{\partial H}{\partial q} - \frac{\zeta p}{Q}\\ \dot{q} &= \frac{\partial H}{\partial p}\\ \dot{\zeta} &= p^2 - \frac{1}{\beta}\\ \dot{\eta} &= \frac{\zeta}{\beta Q} \end{aligned}\]これは能勢のハミルトニアンから変数変換された運動方程式に一致する。上記の微分方程式系において、
\[H_\mathrm{c} = H + \frac{\zeta^2}{2Q} + \eta\]が第一積分となることを確認するのは容易であろう。
Kinetic-Moments法
Kinetic-Moments法の運動方程式は以下の通り。
\[\begin{aligned} \dot{p} &= - \frac{\partial H}{\partial q} - \frac{\zeta p}{Q_\zeta} - \frac{\eta p^3}{Q_\eta}\\ \dot{q} &= \frac{\partial H}{\partial p}\\ \dot{\zeta} &= p^2 - \frac{1}{\beta} \\ \dot{\eta} &= p^4 - \frac{3 p^2}{\beta} \end{aligned}\]この運動方程式は、以下の拡張ハミルトニアン$H_\mathrm{ex}$について温度$\beta$のカノニカル分布を定常状態に持つ。
\[H_\mathrm{ex} = H + \frac{\zeta^2}{2Q_\zeta}+\frac{\eta^2}{2Q_\eta}\]さて、Nose-Hoover法の時と同様に、新たな追加自由度$\theta$を導入し、
\[H_\mathrm{c} = H_\mathrm{ex} + \theta\]とする。ここで$\dot{H}_\mathrm{c} = 0$という条件から$\dot{\theta}$を定めることができる。全体の運動方程式は以下のようになる。
\[\begin{aligned} \dot{p} &= - \frac{\partial H}{\partial q} - \frac{\zeta p}{Q_\zeta} - \frac{\eta p^3}{Q_\eta}\\ \dot{q} &= \frac{\partial H}{\partial p}\\ \dot{\zeta} &= p^2 - \frac{1}{\beta} \\ \dot{\eta} &= p^4 - \frac{3 p^2}{\beta} \\ \dot{\theta} &= \frac{\zeta}{\beta Q_\zeta} + \frac{3 p^2 \eta}{\beta Q_\eta} \end{aligned}\]Nose-Hoover-Chain法
Nose-Hoover-Chain法の運動方程式は以下の通り。
\[\begin{aligned} \dot{p} &= - \frac{\partial H}{\partial q} - \frac{\zeta p}{Q_\zeta}\\ \dot{q} &= \frac{\partial H}{\partial p}\\ \dot{\zeta} &= p^2 - \frac{1}{\beta} - \frac{\eta \zeta}{Q_\eta} \\ \dot{\eta} &= \frac{\zeta^2}{Q_\zeta} - \frac{1}{\beta} \end{aligned}\]Kinetic-Moments法と同様に追加自由度$\theta$を導入し、Kinetic-Moments法と同じ保存量
\[H_\mathrm{c} = H_\mathrm{ex} + \theta\]を構築すると、以下の運動方程式を得る。
\[\begin{aligned} \dot{p} &= - \frac{\partial H}{\partial q} - \frac{\zeta p}{Q_\zeta}\\ \dot{q} &= \frac{\partial H}{\partial p}\\ \dot{\zeta} &= p^2 - \frac{1}{\beta} - \frac{\eta \zeta}{Q_\eta} \\ \dot{\eta} &= \frac{\zeta^2}{Q_\zeta} - \frac{1}{\beta}\\ \dot{\theta} &= \frac{\zeta}{\beta Q_\zeta} + \frac{\eta}{\beta Q_\eta} \end{aligned}\]数値計算
以上、それぞれ構築した保存量を使って、微分方程式の精度を確認することができる。調和振動子にKinetic-Moments (KM)法とNose-Hoover-Chain (NHC)法を適用した結果を示す。Nose-Hoover法は調和振動子を正しく温度制御できないので、ここでは省く。それぞれ1次のEuler法と4次のRunge-Kutta法で時間発展させた結果である。設定温度は$1$、熱浴質量は、Kinetic-Momentsで$(Q_\zeta, Q_\eta) = (4,6)$、Nose-Hoover-Chain法で$(2,5)$とした2。
保存量の時間発展
まずKinetic Moments法の保存量の時間発展(両対数グラフ)。
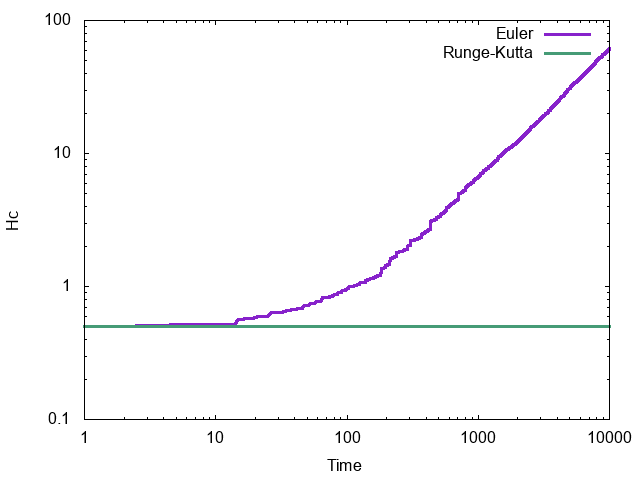
次がNose-Hoover-Chain法の保存量の時間発展(両対数グラフ)。
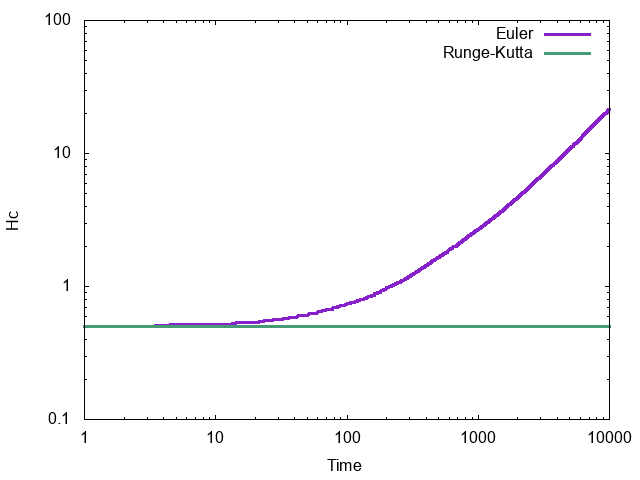
いずれもRunge-Kuttaでは保存量が正しく保存しているのにたいし、1次のEulerでは時間に比例してずれていくことがわかる。
カノニカル分布
調和振動子系のエネルギー$E = p^2/ + q^2/2$について、累積分布関数をプロットしてみる。
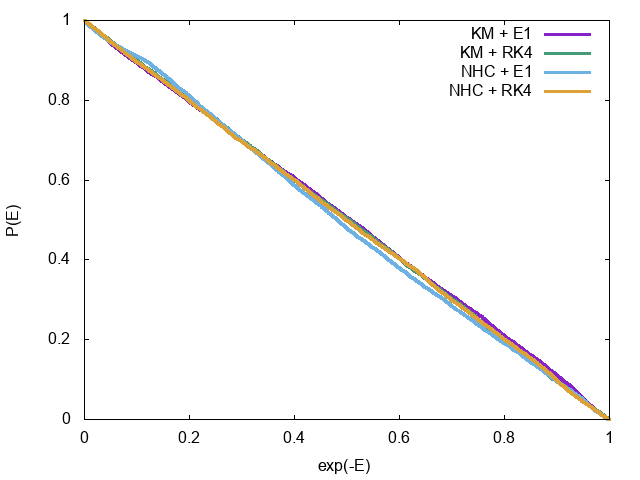
累積分布関数を$\exp(-E)$についてプロットしているため、結果が(1,0)と(0,1)を結ぶ直線になれば正しくカノニカル分布が実現している。これを見るとわかるように、精度の悪いスキームで時間発展させ、保存量が保存していない場合でも、エネルギーのゆらぎはカノニカル分布に従っている。
まとめ
Nose-Hoover法と同様な保存量を、Kinetic-Moments法やNose-Hoover-Chain法などの多変数熱浴について構築した。低精度の積分スキームを用いると、保存すべき量が保存していないことがわかる。しかし、その場合でもエネルギーのゆらぎは指定温度のカノニカル分布に従っている。一般に熱浴がついた系では、熱浴が全エネルギーを制御するためにエネルギーのドリフトが起きにくく、積分スキームがいいかげんでもそれなりに計算できることが多い。無論、低精度の積分スキーム用いた場合は分子の軌道は全く信用できなくなるが、熱浴をつける場合は個々の分子の軌道そのものに興味が無いことが多いし、そもそも熱浴をつけた系における運動方程式の軌道が何を意味するかは微妙な気がする。
だから積分スキームはいいかげんで良い、というつもりはないが、とりあえず熱浴をつけた場合でも保存量は簡単に構築できるため、自分の計算がどのくらいの精度があるかを一度は確認しておいた方が良い。
上記の計算に使ったソースを
https://github.com/kaityo256/thermostats
においておく。
 A Robot’s Sigh
A Robot’s Sigh