分子動力学法ステップ・バイ・ステップ その5
分子動力学法ステップ・バイ・ステップ その5
はじめに
Step 4までで、一通りMDを書き終わった。しかし、実用的に使うためには温度制御が必須である。以下では温度制御法を幾つか実装する。
今回のコードはgithub/kaityo256/mdstep/step5においてあるので、適宜参照されたい。
注意:ここに書いてある温度制御法の説明はかなり適当なので、実装方法以外はあまり真面目に考えないこと。
- その1 $O(N^2)$のルーチンまで
- その2 ペアリストの構築とBookkeeping法
- その3 メッシュ探索
- その4 少しだけ高速化
- その5 温度制御法を三種類実装してみる ← イマココ
- その6 圧力測定ルーチンの実装
温度制御について
通常、分子動力学法ではハミルトンの運動方程式を数値積分する。するとエネルギーが保存量となるため、得られるアンサンブルはNVEアンサンブルとなる。そこで初期エネルギーEで物理量を測定し、初期条件を変えることを繰り返せば、物理量Aの全エネルギー依存性A(E)が求まる。しかし、一般に興味あるのは物理量のエネルギー依存性ではなく、温度依存性であることが多い。
ある程度大きな系であれば揺らぎはあまり重要では無いため、ある温度Tに対応する全エネルギーEさえ知っていれば、そのエネルギーからスタートすれば温度Tにおける物理量の期待値が得られる。しかし、一般に温度TとエネルギーEの関係は事前にはわからない1。そこで、何かしらの方法で温度を制御する方法が必要となる。以下、いくつか有名な方法を実装してみる。
以下、計算のパラメータは以下の通り。
- システムサイズ L=50
- 原子数 N =62500
- カットオフ 2.0
- 時間刻み dt = 0.01
- 目的温度 1.0
速度スケーリング法
速度スケーリング法(Velocity Scaling method)とは、毎ステップ、もしくは何ステップかごとに、速度の分散を、指定の温度に対応するように無理やりスケールしてしまう方法である。
やり方は極めて簡単で、現在の温度を$T$、目的の温度を$T_a$として、$\sqrt{T_a/T}$を運動量にかけてやる。すると、速度の分散が、温度$T_a$の時のマクスウェル分布の分散と等しくなる。具体的なコードはこんな感じになる。
void
MD::velocity_scaling(const double aimed_temperature){
double t = obs->temperature(vars);
double ratio = sqrt(aimed_temperature/t);
for(auto &a: vars->atoms){
a.px *= ratio;
a.py *= ratio;
a.pz *= ratio;
}
}
これを毎ステップ呼んでやると、見かけ上温度が指定温度に固定される。するとそのうちポテンシャルエネルギーも緩和して行き、最終的には指定温度におけるポテンシャルエネルギーに等しくなるであろう、という方法である。実行結果は以下の通り。
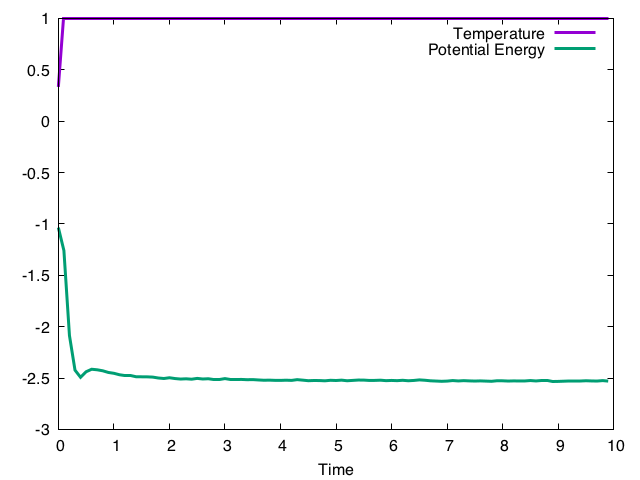
系の温度を速度の分散で定義しているため、定義上、温度はすぐに指定温度である1.0にぴたっとはり付く。ポテンシャルエネルギーはゆっくり緩和していき、およそt = 10程度で緩和していると思われる。
似た発想の温度制御法としてガウシアン法(Gaussian Thermostat)というのがある。名前から確率的熱浴と誤解されることが多いのだが、これは乱数を使わない決定論的手法で、「運動エネルギーの合計が指定温度に対応する値に固定される」という拘束条件を課して変分を取ることで得られる運動方程式を解く。こちらも運動エネルギーは全く変化せず、そのうちポテンシャルエネルギーが指定温度での値に緩和するだろう、という方法である。
ランジュバン法
広く使われている方法として、ランジュバン法(Langevin method)という方法がある。これは、運動方程式に摩擦項と揺動項を付け加えてランジュバン方程式にすることで指定の温度に緩和させるというものである。運動方程式はこのような形になる。
\[\dot{p} = - \frac{\partial H}{\partial q} - \gamma p + R\\ \dot{q} = \frac{\partial H}{\partial p}\]ただし$R$は平均ゼロ、$\left< R(0)R(t) \right> = 2D \delta(t) $を満たすような要動力である。$D$と$\gamma$の比が温度を与える(アインシュタインの関係式)。そこで、$\gamma$の値を決めておくと、目的温度から$D$の値が決まる。時間による離散化も考慮すると、以下のようなコードになる。
void
MD::langevin(const double aimed_temperature){
static std::mt19937 mt(1);
const double gamma = 1.0;
const double T = aimed_temperature;
const double D = sqrt(2.0 * gamma * T /dt);
std::normal_distribution<double> nd(0.0, D);
for(auto &a: vars->atoms){
a.px += (-gamma * a.px + nd(mt)) * dt;
a.py += (-gamma * a.py + nd(mt)) * dt;
a.pz += (-gamma * a.pz + nd(mt)) * dt;
}
}
文中にあらわれる(-gamma * a.px + nd(mt)) * dtの部分が、ランジュバン方程式の$- \gamma p + R$に対応する。$\gamma$は自由パラメータになるが、これが指定温度への緩和時間を決める。この例のように1.0にした場合の結果は以下の通り。
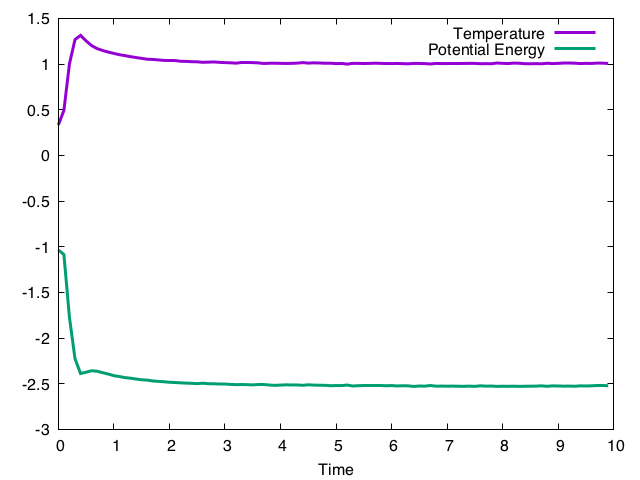
温度がゆっくり指定温度に緩和していき、ポテンシャルエネルギーも速度スケーリングの場合と同じ値(-2.5)に緩和していくように見る。
Nose-Hoover法
ランジュバン法は乱数を用いたが、決定論的な手法としてNose-Hoover法が広く使われている。この手法は、運動方程式を以下のように書き換える。
\[\dot{p} = - \frac{\partial H}{\partial q} - \zeta p\\ \dot{q} = \frac{\partial H}{\partial p}\\ \dot{\zeta} = \frac{1}{\tau^2}(T - T_a)\]ただし$T$が現在の温度、$T_a$が目的の温度である。これを運動方程式に落とす際、シンプレクティック積分に似た数値積分も適用可能なのだが2、ここでは手抜きで温度制御のところだけ1次のオイラー法で組んでしまおう。
void
MD::nosehoover(const double aimed_temperature){
double t = obs->temperature(vars);
double at = aimed_temperature;
double tau = 0.1;
vars->zeta += (t - at)/ (tau * tau)*dt;
for(auto &a: vars->atoms){
a.px -= a.px * vars->zeta*dt;
a.py -= a.py * vars->zeta*dt;
a.pz -= a.pz * vars->zeta*dt;
}
}
これを毎ステップ呼んでやれば温度が制御される。自由パラメータはtauだが、これが指定温度への緩和時間を決める。実行結果は以下の通り。
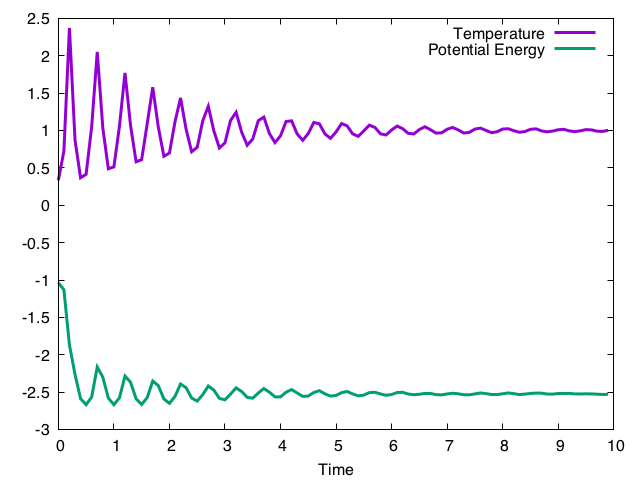
ランジュバン法と異なり、温度が振動しながら目的の値に緩和していくのがわかる。それにつられてポテンシャルエネルギーも振動するが、やがて他の手法と同じ値(-2.5)に緩和してく。
まとめ
温度制御の方法をみっつほど実装してみた。指定の温度に無理やりしてしまう速度スケーリング法、乱数を使って緩和させていくランジュバン法、振動しながら緩和させるNose-Hoover法が広く使われている。Nose-Hoover法は補助変数$\zeta$を介して温度制御を行うが、補助変数無しで制御するベレンゼン法(Berendsen thermostat)も広く使われている。ベレンゼン法の場合はランジュバン法のように温度が指数関数的に緩和していく性質がある。
このうち、運動エネルギーとポテンシャルエネルギーを含めた系全体の定常状態が、厳密に指定温度のカノニカル分布になるのはランジュバン法とNose-Hoover法だけなのだが、結局のところ重要なのは「ポテンシャルエネルギーが指定温度における期待値に緩和していること」なので、そこだけ気をつけていれば速度スケーリング法のような野蛮(?)な方法を使っても問題ないと思う。逆に、運動温度のみ確認して、ポテンシャルエネルギーが緩和していないのに「緩和した」と思ってしまうほうがまずいので、絶対にポテンシャルエネルギーの緩和を見る必要がある速度スケーリング法やガウシアン法の方がそういう意味では安全と言えなくもない。
ここまでのコードはgithub/kaityo256/mdstep/step5においてある。
 A Robot’s Sigh
A Robot’s Sigh