極小ヒッティングセットを列挙する(枝刈り工夫版)

はじめに

与えられた入力に対して、極小ヒッティングセット(minimal hitting set)¹を列挙するニーズがあった。一応Rubyで書いてみたが速度的にアレなので、C++で、かつビット演算を使い、枝刈りも工夫してみたい。

本稿で書いたコードは https://github.com/kaityo256/mhs_cpp にある。

用語のまとめ

極小ヒッティングセット

あるビット列の組が与えられたとする。このビット列の全てと論理積(AND)をとってゼロで無いようなビット列をヒッティングセット(hitting set, HS)と呼ぶ。また、他のヒッティングセットを真部分集合として含まないようなものを極小ヒッティングセット(minimal hitting set, 以下MHS)と呼ぶ。具体例については以前の記事を参照。

k-MHS

いま、N個の入力データがあるとする。その集合を$E　= \{e_1, e_2, \cdots, e_N \}$とする。この時、最初の要素から$k$番目までの部分集合を$E_k$と呼ぶ。$E_k = \{e_1, e_2, \cdots, e_k \}$である。そして、$E_k$に対するヒッティングセットをk-HS、特にそのうち極小であるものをk-MHSと呼ぶ。明らかに k-MHSは、(k+1)-MHSに含まれる。

逆探索と親子関係

いま、MHSに親子関係を定義する。あるビット列$t$がk-MHSであったとする。この時、このビット列の「親」を以下のように定義する。

もし、そのビット列が(k-1)-MHSであったなら、親は自分自身とする。
そうでなければ、ビット列から1ビットを取り除けば(k-1)-MHSとなるので、それを親とする。

項目2について補足。あるビット列$t$がk-MHSであったのだから、そのビット列のどのビットが欠けても、重なりのない(ANDをとってゼロになる)要素が出てきてしまう。しかし、それが$k-1$-MHSではない、つまり$e_k$を除くと、$t$は極小ではなくなるのだから、$t$と$e_k$は1ビットでのみ重なりを持っているはずである²。そのビットを取り除くと、$t$は(k-1)-MHSになるはずであり、これを親とする。

上記により、任意のk-MHSであるようなビット列には親が一意的に定まる。複数の子が親を共有することはあっても親が子を共有することは無いので、この親子関係は木となる。

全てのビットが0であるようなビット列は、0-MHSとみなすことができる。これを始点とし、1-MHS、2-MHSと調べて行く。N-MHSが求めるものである。

こうして木構造を持つ親子関係を定義し、根から全て探索していく方法が逆探索(Reverse Search Algorithm)である。

E = {011, 110}の場合を図解するとこんな感じ。

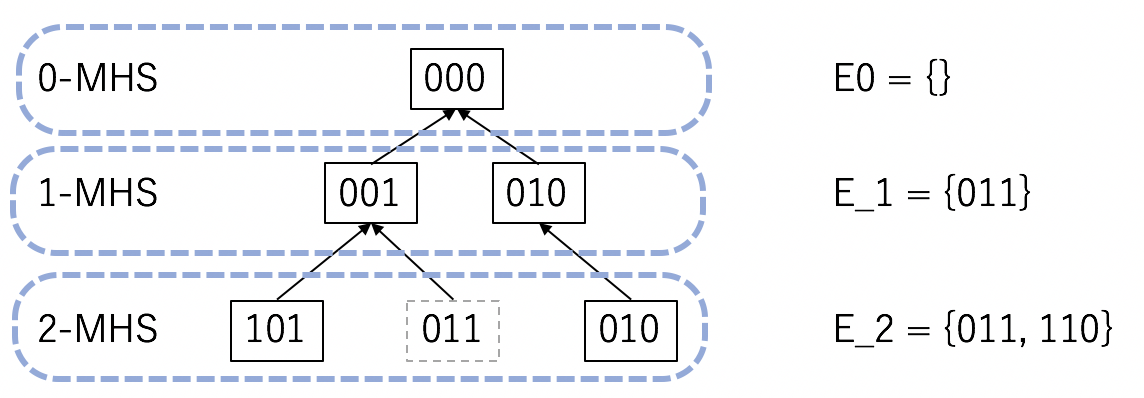
最初に「000」からスタートする。
「000」は「011」と重なりを持たないので、「011」のビットのいずれかをもらって再帰する。
右側の枝「010」に行った場合、それは「110」とも重なりを持つので、そのまま採用される。
左側の枝「001」は「110」と重なりを持たないので、「110」のビットのいずれかをもらって再帰
「101」は極小なのでそのまま採用するが、「011」は、他のヒッティングセット「010」を真部分集合として持つから極小ではない。なので不採用
以上の手続きを経て、2-MHSとして「101」「010」を得る。

再帰プログラムは簡単で、C++でコードを書くならこんな感じになるだろう。あとで32ビット以上に拡張することを見越して、int32_tをmybitに、そのvectorをmybitsにtypedefしておこう(なんか良い名前じゃない気がするが細けぇこたぁいいんだよ！)。

typedef int32_t mybit;
typedef std::vector<mybit> mybits;

void
search(int k, mybit t, mybits &e, mybits &r) {
  if (k == e.size()) {
    r.push_back(t);
    return;
  }
  if (t & e[k]) {
    search(k + 1, t, e, r);
  } else {
    mybit v = e[k];
    while (v) {
      mybit t2 = v & -v;
      if (check_minimal(t|t2, k+1, e)){
        search(k + 1, t | t2, e, r);
      }
      v = v ^ t2;
    }
  }
}

eが入力、rが出力である。　k-MHSであるビット列$t$が渡されてくるので、それが$e_{k+1}$ = e[k]と交わりがあるか調べ²、交わっていればそのまま再帰、そうでなければビットを追加して再帰する。

プログラムは非常に単純だが、問題は極小条件判定check_minimalである。前置きが長くなったが、これをなんとかしましょう、というのが本稿の主題である。

極小条件判定

ナイーブな方法

あるk-HSなビット列$t$が、極小であるかどうかを調べたい。極小であるとは、要するにどのビットが欠けてもヒッティングセットでなくなるということなのであるから、実際に1個ビットを削ってみて、$E_k$の要素全てとチェックし、もし全てと重なりがあったら極小でない、という判定が考えられる。こんな感じ。

bool
check_minimal(mybit t, int k, mybits &e) {
  mybit v = t;
  while (v) {
    mybit t2 = v & -v;
    mybit t3 = t ^ t2;
    bool flag = true;
    for (int i = 0; i < k; i++) {
      flag &= ((e[i] & t3) != 0);
      if(!flag)break;
    }
    if (flag)return false;
    v = v ^ t2;
  }
  return true;
}

この方法では、ビット列の長さを$B$として、計算量が$O(kB)$となる。これを削減したい。

Critical hyperedgeを使った方法

k-MHSであるビット列$t$を考える。定義によりこのビット列は$E_k$の要素全てと重なりを持つはずである。さて、ある要素$e_i$が、ビット列$t$のただ一つのビット$t_j$と重なりを持っているとする。この時、$e_i$はこのビットのcritical hyperedgeであると定義する。要するに「このビットを消したら、カバーできなくなる要素」のことである。

ビット列$t$がMHSであるとは、「どのビットが欠けても重なりを持たない要素が出てくる」というのが定義であるから、ビット列$t$の全ての立っているビットには、それにぶら下がるcritical hyperedgeがいるはずである。もしcritical hyperedgeが存在しないビットが立っていたら、それを除いてもまだ要素全てと重なりを持てるので、ビット列$t$がMHSであることと矛盾する。こうして、k-MHSのビット列$t$の各ビットには、それぞれ一つ以上のcritical hyperedgeがぶら下がっている。

さて、いま(k-1)-MHSであるビット列$t$が、$e_k$と重なりを持たなかったとする。この時、$e_k$に含まれるビット$t’$を一つ$t$に立ててk-MHSの候補を作るのだが、この時、既存のビットにぶら下がるcritical hyperedgeは減ることはあっても増えることは無い。したがって、この操作でcritical hyperedgeがなくなったビットが出現した瞬間、$t

t’$は極小でないことがわかる。

以下に例を図示する。

上の段が入力$E$、下の赤で囲まれたビット列がMHS候補の$t$である。$e_i$が$t$とただ一つのビット$t_j$で交わる場合、そのビットを赤くしておく。赤いビットを持つ要素は、そのビットのcritical hyperedgeであり、$t$の全てのビットにcritical hyperedgeがぶら下がっている場合、$t$は極小となる。また、$t$と２つ以上のビットで交わる要素(青く示す)も存在するが、これはcritical hyperedgeにはならない。

左が極小の場合、右がそうでない場合。右には、critical hyperedgeがぶら下がっていないビットが含まれ、それを削除しても全ての要素と重なりを持てる。したがってMHSではない。

再帰していく間、critical hyperedgeの対応関係を覚えておき、新たなビットが追加された時点でcritical hyperedgeがなくなったビットがいたら、その時点で再帰の枝刈りができる。これが参考文献に記載されているcritical hyperedgeを用いた枝刈りである(たぶん)。

Critical hyperedgeのビット演算による判定

さて、再帰の間、ビット列とcritical hyperedgeの対応関係を覚えておくのは面倒である。再帰するので、対応表をコピーするか、同じ表を使いまわさないといけない。というわけで、ビット列とcritical hyperedgeの対応関係をその場で計算することを考える。

$t$が極小ヒッティングセットである場合には、全てのビットがcritical hyperedgeを持っていることであるから、逆に$t$と1ビットだけで重なりを持つ場合、そのビットの集合が$t$と一致する、というのが極小条件である。

minimalな場合はこんな感じに一致する。

minimalでない場合は、左右が一致しない。

したがって、e[i]とtの論理積を取って、重なりが1ビットだけのビット列全ての論理和(OR)を取り、できたビット列がもともとの$t$と一致するか確認すれば良い。おそらくコードを見たほうが早い。

bool
check_minimal2(mybit t, int k, mybits &e) {
  mybit t2 = 0;
  for (int i = 0; i < k; i++) {
    if (popcnt(t & e[i]) == 1) {
      t2 = t2 | (t & e[i]);
    }
  }
  return (t2 == t);
}

先のコードよりもだいぶ簡単になった。 popcntは、例えば

int popcnt(mybit v) {
  return __builtin_popcount(v);
}

とかすればいいんじゃないでしょうか(要emmintrin.h)。チェックの時間は$O(k)$となる³。もちろん、前回やった情報を覚えておいて、今回更新のあるところだけ調べる方が計算量は落ちるんだけど、命令がビット演算とpopcntしかなくて、しかも入力データはどうせキャッシュにのるだろうから⁴、毎回計算しちゃったほうが早いんじゃないかなぁ。

テスト

リポジトリに、テストデータ作成用のスクリプトgen.rbを用意した。

$ ruby gen.rb 32 10 200  > input.dat

これは、32ビットのうち10ビットだけ立ってるビット列を200個用意する。これを先のコードに食わせるが、解の出力はしないで、解の個数だけ出力するようにしておこう。

テスト環境は以下の通り。

iMac (Retina 5K, Late 2015)
3.3 GHz Intel Core i5
メモリ 8GB 1867 Mhz DDR3
g++ (Homebrew GCC 6.3.0_1) 6.3.0
コンパイルオプション -O3 -mavx -mavx2

計算結果はこんな感じ。

手法	時間[s]
ナイーブな極小条件判定	3.621
CHを使った判定	2.396
shd (-O3 -Os -s)	2.811
shd (-O3 -mavx -mavx2 )	2.052

shdというのは、参考にした論文の著者によるプログラム。gen.rbはこのプログラムと互換性のある入力ファイルを出力できるようになっている。

ナイーブな方法(check_minimal)では3.621秒だったのが、改良された枝刈り(check_minimal2)では2.396秒まで落ちたので、効果はあった。なお、同じ入力にたいしてshdが最初2.811秒とかかかったので「勝った！」と思ったのだが、普通にmakeするとコンパイルオプションが-O3 -Os -sと古い感じになってて、同じにしないと不公平だと思って-O3 -mavx -mavx2で再コンパイルしたら負けた・・・　○ ￣＿

まとめ

ヒッティングセット、すなわち与えられたビット列全てと重なりを持つ(論理積をとって0でない)ビット列を列挙するプログラムを書いた。ビット演算を使うのが自然だと思うので、一応フルにビット演算で書いてみたら、まぁまぁ満足できる速度が出た。int32_t使ってるから32ビットまでしか対応できないが、昨今の環境なら128ビットまでは特に苦労なく拡張できるんじゃないかなぁ。

本稿で書いたコードを https://github.com/kaityo256/mhs_cpp においておくので、自由に高速化とか高速化とかしてください＞ビット演算系人外の皆様

参考文献

本稿の執筆は主に以下の論文を参考にした。

Efficient algorithms for dualizing large-scale hypergraphs
- Keisuke Murakami and Takeaki Uno
- Discrete Applied Mathematics
- Volume 170, 19 June 2014, Pages 83–94
- http://dx.doi.org/10.1016/j.dam.2014.01.012
上記の著者によるプログラム
- http://research.nii.ac.jp/~uno/code/shd.html
- http://research.nii.ac.jp/~uno/codes.htm

普通のグラフでは頂点被覆(vertex cover)と呼ぶようだが、ここで扱うハイパーグラフではヒッティングセット(hitting set)の方が一般的みたい。 ↩
C/C++の配列が0スタートなのと、k-MHSのｋが1スタートなのでインデックスが一つずれることに注意。 ↩ ↩²
論文を読む限り、論文に記載されたアルゴリズムと同じ計算オーダーになってるはずだ思うんだけど、あまり自信がない。 ↩
これは典型的なNPの問題であり、入力データに対して計算量が爆発的に増えるため、あまり大きなデータを食わせることはできない。 ↩