極小頂点被覆を列挙する

はじめに

与えられた入力に対して、極小頂点被覆(minimal hitting set)を列挙したい。で、ネットなり参考文献なりを探したんだけど、なんかどれも妙に難しくて「もっと俺みたいなアホにもわかるように書いてくれ！」¹ と思ったので、自分の理解の確認も含めて以下に雑にまとめる。

出て来るコードは https://github.com/kaityo256/hs_ruby においてある。

なお、私はド素人なので、以下はいろいろ間違いや思い違いがあるかも(逃げ)。

頂点被覆とは

頂点被覆については、グラフ理論の枠組みで語られることが多い。例えばWikipediaの記述はそうなっている。でも、プログラマにとってはビット演算で考えた方がわかりやすいと思う。

以下のようなビット列の集合が与えられたとする。

110
011

これらすべてとAND(論理積)をとって0にならないようなビット列を頂点被覆(hitting set)と呼ぶ。この例だと

は全て頂点被覆である。このうち「他の頂点被覆を真部分集合として含まないもの」が極小頂点被覆(minimal hitting set)である。「最小」ではないことに注意。例えば「111」は頂点被覆だが、真部分集合として「101」や「010」を含むので極小頂点被覆ではない。

上記の例だと、

010
101

が極小頂点被覆である。グラフの方がわかりやすい人のために図示するとこんな感じ。全ての辺が、選んだ頂点(赤丸)とつながるように赤丸を選んでいる。

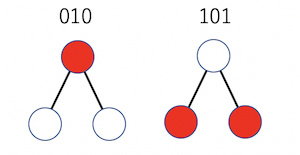
このうち、要素数が最小のもの(左の方)を最小頂点被覆(minimum hitting set)と呼ぶが、ここではそれは扱わない。

さて、これを任意のビット列の集合にたいして極小頂点被覆を列挙したい、というのが本稿の主題である。

ナイーブな方法

極めてナイーブには、ビット列の配列を上からなめていって、

現在のビット列と重なりがあれば次へ
重なりがなければ、そのビット列から1ビット加えて再帰
配列の最後まで行ったらおしまい

といったアルゴリズムを思いつくであろう。

それを素直に実装するとこうなるかと思う。kがいま調べてる要素の位置、tが現在のビット列、eが入力の配列、rが解の配列である。

def search(k, t, e, r)
  if k == e.size
    r.push t
    return
  end
  if (t & e[k]) !=0
    search(k+1,t,e,r)
    return
  end
  v = e[k]
  while v!=0
    t2 = v & -v
    search(k + 1, t | t2, e,r)
    v = v ^ t2
  end
end

これに

110
011

を食わせる。こんな感じ。

e = [6,3]
search(0,0,e,r)
p r

この結果、得られる出力は

010
101
110

となり、極小でない頂点被覆「110」を含んでしまう。これは、

・最初に「110」のうち「100」を選び、・次に「011」と交わりを得るために「010」を追加する

というパスがあるため。また、このナイーブな方法だと、同じビット列をなんども出力してしまう場合もある。これをなんとかするのが逆探索の考え方である。

極小頂点被覆列挙への逆探索の適用

逆探索とは

逆探索の基本的な考え方は、解の集合に一意な親子関係を作ることにある。ある解$B$に対し、その親を$p(B)$で定める。ただし、$B$自身が自分の祖先にならないようにする。これにより、親子関係は必ず木となる。この木を列挙木と呼ぶ。ある解の親が一意に決まるようにすれば、列挙木の同じ深さに同じ解が出現しない(重複しない)ことが保証される(ただし後で見るように、異なる深さには同じ解が出現し得る)。これを適当な初期解$B_0$から深さ優先探索をして解を列挙しよう、というアルゴリズムである。

親子関係の定義

後のため、いくつか用語と記号を定義しておく。

入力の集合を$E$で表し、その要素を$E = \{ e_1, e_2, \cdots, e_n \} $で表す。

以下の入力データ

110
011

であれば、$e_1 = $ 110, $e_2 = $ 011である。

$E$の、$k$番目までの要素を持つ部分集合を$E_k$とする²。先の例なら、$E_1 = \{e_1\}$、$E_2 = \{e_1, e_2\}$である。

さて、ある$E_k$に対して、ビット列$t$が極小頂点被覆であるとき、これを$k$極小頂点被覆と呼ぶ。

ある$k$極小頂点被覆ビット列$t$の親$p(t)$を以下のように定める。

もし$t$が$k-1$極小頂点被覆であるならば $p(t) = t$
そうでない場合は、$t$から一つビットを外して$k-1$極小頂点被覆となったものを親とする

これが親を一意に決めることを見よう。

まず、$t$が$k-1$極小頂点被覆でもあるなら、親は$t$であるから一意に決まる。

次に、$t$が$k-1$極小頂点被覆でない時を考える。$t$は$k$極小頂点被覆であったから、どのビットが欠けたとしても$\{e_1, e_2, \cdots, e_k\}$と論理積をとって0でない、という条件を満たせない。

しかし、$t$は$k-1$極小頂点被覆でないのだから、どこかのビットを消しても$\{e_1, e_2, \cdots, e_{k-1}\}$の頂点被覆となり得る。その「消せるビット」は一つだけのはずであるため、一意に決まる³。したがって、$t$から「消せるビット」を消した親も一意に決まる。

例を挙げよう。以下のような4要素の入力を考える。

この入力に対する4極小被覆は明らかに111である。さて、4極小被覆である111の親(3極小被覆)を考える。$E_3$にあたるのは上から３つまでのデータなので

110
100
010

である。これに対して、「111」は極小ではない。これに対する極小被覆は「110」であることから「111」の親は「110」となった。

同様に、$E_2$を考える。

110
100

これに対して、「110」は極小でない。2極小被覆は「100」となる。

$E_１$は「110」であり、「100」は1極小被覆であるから、「100」の親は「100」となる。

以上をまとめると、1極小被覆から順番に

100 ← 100 ← 110 ← 111

という親子関係(矢印は親←子)が結ばれた。

さて、これを逆にたどることで全部の$k$極小頂点被覆を列挙することができる。このうち、木の一番深いところだけを表示したものが、求める極小頂点被覆である。

子をたどる方法

さて、親子関係が定義できたら、列挙木をたどる方法は簡単である。最初に$t=000$としておいて、1極小頂点被覆から順番に4極小頂点被覆まで調べていけば良い。

また以下のデータを考える。

最初のデータが$e_1$=110なので、1極小頂点被覆の選択肢としては「100」と「010」が考えられる。

最初に「100」を選んだ場合は、

100 ← 100 ← 110 ← 111

と、答えが得られる。それぞれが$k$極小頂点被覆となっていることに注意。

問題は最初に「010」を選んだ場合だが、次のデータ($e_2$)が「100」なので、頂点被覆するためには「110」にしなければならない。しかし、これは他の頂点被覆「100」を真部分集合として含むため、2極小頂点被覆ではない。列挙木の深さ$k$の葉は、全て$k$極小被覆被覆でなければならないのだから、これは採択できず、これ以上再帰できない。

実装

以上を実装するのはすこぶる簡単である。最初に作ったナイーブな再帰に対して、$k$極小頂点被覆であるかどうかを確認し、もし違ったらそこで再帰をやめれば良い。

与えられたビット列$t$が$k$頂点被覆であるかどうかは以下のような処理になろう。

def check_minimal(t,k,e)
  v = t
  while v!=0
    t2 = v & -v
    t3 = t ^ t2
    if e.slice(0..(k-1)).collect{|ei| (ei & t3)!=0}.inject(:&)
      return false
    end
    v = v ^ t2
  end
  return true
end

単純に$t$から一個ビットを消したものに対して、$k$番目までの要素と論理積をとって、もし全ての要素と交わりがあったら、それは極小頂点被覆でないということなので偽を返す関数である。これを再帰の直前でチェックし、極小性を満たすものだけ再帰するように修正すれば良い。

def search(k, t, e, r)
  if k == e.size
    r.push t
    return
  end
  if (t & e[k]) !=0
    search(k+1,t,e,r)
    return
  end
  v = e[k]
  while v!=0
    t2 = v & -v
    if check_minimal(t|t2,k+1,e) # 極小性チェックを追加
      search(k + 1, t | t2, e,r)
    end
    v = v ^ t2
  end
end

まとめ

極小頂点被覆を列挙するコードを書いた。世の中にあるサンプルや解説がほとんど「重み付き」の問題で、それを線形計画とかでどうこうする奴で、僕には理解が難しかったので、過去の自分にわかるように書いたつもり。なお、高速化については参考文献やさらにその参考文献を参照されたい。

参考文献

主に以下の解説を参考にした。

宇野毅明：極小集合被覆を列挙する実用的高速アルゴリズム(PDF)

また、本稿のサンプルコードを https://github.com/kaityo256/hs_ruby においておくので参考にされたい。

個人的には具体例が少ないのが理解の妨げとなった。 ↩
参考文献では$k$の代わりに$i$を使っているので注意。 ↩
「消せるビットが一つしかない」というのは直感的には明らかだと思うが、ちゃんとした証明は参考文献を参照のこと。なお、消せるビットはk番目の要素とtの論理積で得られる。 ↩