ナンプレの正規化 ステップ・バイ・ステップ その1
ナンプレの正規化 ステップ・バイ・ステップ その1
はじめに
ナンプレ(数独とも)は、9×9のマスの中に決められた条件を満たすように1から9の数字を埋めていくパズルで、多くの愛好者がいる。さて、ナンプレは行や列の入れ替え、置換、数字の入れ替えなどで新たな問題を多数作ることができる。ナンプレ作家なら、何か問題を作った時に「これ、以前作った奴かな?」と思うことがあるだろう。その時に必要になるのがナンプレの正規化である。正規化とは、等価な問題なら必ず同じ問題に落ちるようにする変換のことである。正規化にはいくつか種類があるが、ここでは「ナンプレを81桁の整数とみなした際に最も値が小さくなる」ような問題を正規化された問題と呼ぶ。で、とある事情でナンプレの正規化をすることになったんだけど、後で自分が何やったか覚えている自信が全くないのでメモ1。
例えば
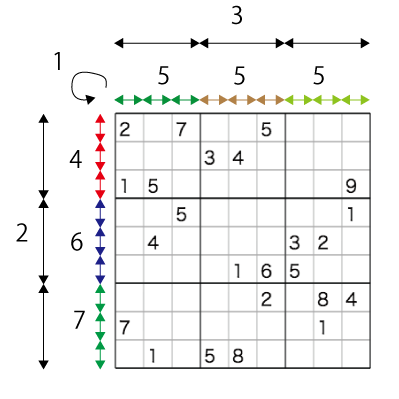
207005000000340000150000009005000001040000320000016500000002084700000010010580000
を食わせた時に、
000000012000034005006007300001300007053080000080000100010005090200100000700400030
が出力として返ってくるようなプログラムを組む。
ソースコードは以下に置いてある。 https://github.com/kaityo256/minlex
ナンプレの対称操作
ナンプレは、問題の本質を変えない対称操作がいくつかある。 そのため、用語を定義する(一般的な用語かどうかは知らない)。
- 3×3のブロックを「ボックス」と呼ぶ。
- 上から三行ずつまとめた行を「ボックス行」と呼ぶ。3つのボックス行がある。
- 特に、一番上のボックス行を「ヘッドボックス」と呼ぶ。
- 左から三列ずつまとめた列を「ボックス列」と呼ぶ。3つのボックス列がある。
すると、ナンプレで許される対称操作は以下の通り。
- 転置 $2$
- ボックス行同士の入れ替え $6$
- ボックス列同士の入れ替え $6$
- ボックス行内の行の入れ替え $6^3$
- ボックス列内の列の入れ替え $6^3$
- 数字の入れ替え $9!$
全部合わせると1218998108160通りで、枝刈りいれても全探索はしんどい感じ。なので真面目にやる2。
対称操作の順番
とりあえずは最低限の枝刈りだけでやる3。まずヘッドボックスを確定させて、そこを中間地点としよう。すると、headbox、つまり元の数字の最初の27桁が決まっているので、その時点で見つかっている最小のheadboxよりも大きい場合はそれ以上調べる必要はない。先にheadboxを確定させるために、以下のような順番で入れ替えを実行する。
- 転置
- ボックス行の入れ替え
- ボックス列の入れ替え
- ヘッドボックス内の行の入れ替え
- ボックス内の行の入れ替え (この時点でヘッドボックスの数字が確定)
- 二段目のボックス行内の行の入れ替え
- 三段目のボックス行内の行の入れ替え
枝刈りですが、まず5. まで終わった段階で数字を出現順に振り直します。ここでヘッドボックス内の数字が確定するため、この時点で見つかっているヘッドボックスの最小の数字(27桁)よりも大きい場合、それ以上探す必要がないために枝刈りができます。
実装
Ruby(文字列)版
まずは全く何も考えずに、ナンプレを81文字の文字列として扱うことにします。
さして長く無いので全文掲載します。
$min = "999999999999999999999999999999999999999999999999999999999999999999999999999999999"
def renumbering(s)
a = Array.new(9){0}
b = "000000000000000000000000000000000000000000000000000000000000000000000000000000000"
index = 0
s.each_byte.with_index do |c,i|
next if c == 48
c = c - 49
if a[c] == 0
index = index + 1
a[c] = index
end
b[i] = (a[c] + 48).chr
end
b
end
def transpose(s)
s2 = ""
9.times do |i|
9. times do |j|
s2 << s[i+j*9]
end
end
s2
end
def transpose2(s)
a = s.each_char.to_a
b = Array.new(81){0}
9.times do |i|
9.times do|j|
b[i+j*9] = a[j+i*9]
end
end
b.join("")
end
def perm_restrbox(s)
sh,sm,sb = s.scan(/.{1,27}/).to_a
sma = sm.scan(/.{1,9}/).to_a
sba = sb.scan(/.{1,9}/).to_a
[0,1,2].permutation do |ai|
si = sma[ai[0]] + sma[ai[1]] + sma[ai[2]]
[0,1,2].permutation do |aj|
sj = sba[aj[0]] + sba[aj[1]] + sba[aj[2]]
ss = renumbering(sh + si + sj)
if ss < $min
$min = ss
end
end
end
end
def perm_columns(s)
st = transpose(s)
sa = st.scan(/.{1,9}/).to_a
[0,1,2].permutation do |ai|
si = sa[ai[0]] + sa[ai[1]] + sa[ai[2]]
[3,4,5].permutation do |aj|
sj = sa[aj[0]] + sa[aj[1]] + sa[aj[2]]
[6,7,8].permutation do |ak|
sk = sa[ak[0]] + sa[ak[1]] + sa[ak[2]]
ss = transpose(si+sj+sk)
ss = renumbering(ss)
next if ss[0..26] > $min[0..26]
perm_restrbox(ss)
end
end
end
end
def perm_toprbox(s)
sh,sm,sb = s.scan(/.{1,27}/).to_a
sa = sh.scan(/.{1,9}/).to_a
[0,1,2].permutation do |ai|
si = sa[ai[0]] + sa[ai[1]] + sa[ai[2]]
si = si + sm + sb
perm_columns(si)
end
end
def perm_cbox(s)
st = transpose(s)
sa = st.scan(/.{1,27}/).to_a
[0,1,2].permutation do |ai|
si = sa[ai[0]] + sa[ai[1]] + sa[ai[2]]
si = transpose(si)
perm_toprbox(si)
end
end
def perm_rbox(s)
sa = s.scan(/.{1,27}/).to_a
[0,1,2].permutation do |ai|
si = sa[ai[0]] + sa[ai[1]] + sa[ai[2]]
perm_cbox(si)
end
end
def search(s)
perm_rbox(s)
perm_rbox(transpose(s))
end
s = "207005000000340000150000009005000001040000320000016500000002084700000010010580000"
ans = "000000012000034005006007300001300007053080000080000100010005090200100000700400030"
puts s
search(s)
puts $min
if $min == ans
puts "OK"
else
puts "NG"
end
順番に
search転置perm_rboxボックス行の入れ替えperm_cboxボックス列の入れ替えperm_torboxヘッドボックス内の行の入れ替えperm_toprbox列の入れ替えperm_restrbox残りのボックス行内の行の入れ替え
という感じ。ここで、4.と6.で数字の振り直し(renumbering)をしている。数字の振り直しは、数字を一番最初から見ていって、出現順に1,2,と振り直すだけなので難しく無いはず。
行の入れ替えをscanでやっている関係から、列の入れ替えを、一度転置して行を入れ替えてまた転置、という無駄なことをやっていますが、気にしないことにする。
さて、適当な入力を入れて実行してみる。
$ time ruby minlex.rb
207005000000340000150000009005000001040000320000016500000002084700000010010580000
000000012000034005006007300001300007053080000080000100010005090200100000700400030
OK
ruby minlex.rb 2.88s user 0.01s system 99% cpu 2.898 total
うーん、一個のナンプレの正規化に3秒近くかかってますね。
Ruby(配列)版
ちゃんとした枝刈りを実装する前に、文字列から配列になおしておきましょう。どうもRubyは文字列のインデックス参照(str[i]みたいなの)がわりとコスト高いみたいなので。
文字列操作が配列操作になるだけなのでスクリプトはほとんど変更を受けない。ただし、そのままでは配列同士の比較ができないので、Comparableをincludeする必要がある。こんな感じ。
class Array
include Comparable
def to_s
self.join("")
end
end
class String
def to_a
self.each_char.map{|c| c.ord - 48}
end
end
ついでに文字列を配列に直すメソッドも追加。あとはscanがsliceになるくらい。
同じ入力を食わせて実行してみる。
$ time ruby array.rb
207005000000340000150000009005000001040000320000016500000002084700000010010580000
000000012000034005006007300001300007053080000080000100010005090200100000700400030
OK
ruby array.rb 1.71s user 0.02s system 99% cpu 1.736 total
うん、まぁまぁ早くなった。
C++版
しかし、一つの問題に秒単位でかかっていては、大量の問題を一度に正規化することはできない。なので枝刈りをちゃんとするわけだが、その前にそのままC++版にしたらどのくらい早くなるかだけ確認しておく。
これはそこそこソースが長いのでリンクを貼るだけにしておく。 https://github.com/kaityo256/minlex/blob/master/step1/minlex.cpp
実行してみる。
$ make
g++ -O3 -std=c++11 -march=native minlex.cpp -o a.out
$ time ./a.out
207005000000340000150000009005000001040000320000016500000002084700000010010580000
000000012000034005006007300001300007053080000080000100010005090200100000700400030
OK
./a.out 0.03s user 0.00s system 83% cpu 0.039 total
さすがに一瞬ですな。
ついでに、適当に作った問題5000問を食わせてみる。
$ wc sample.txt
5000 5000 410000 sample.txt
$ time ./a.out sample.txt > sample.minlex
./a.out sample.txt > sample.minlex 136.91s user 0.42s system 98% cpu 2:19.22 total
5000問の正規化に137秒ですか。さすがにこれは遅い。
まとめ
とりあえず最もナイーブな方法でナンプレの正規化をやってみた。あまりスクリプト言語の速度を気にするのもアレだけど、文字列処理を配列処理に変えるだけでそこそこ早くなるもんですね。あと、C++で書き直したら結構早くなった。ただ、Ruby版では手抜きで行の入れ替えのために転置二回挟んでるけど、C++版はそういう無駄なことはしていないので、適切な比較にはなってないことに注意。
その2へ続く。
 A Robot’s Sigh
A Robot’s Sigh