調和振動子に作用させた熱浴のエルゴード性
調和振動子に作用させた熱浴のエルゴード性
はじめに
分子動力学法(Molecular Dynamics method, MD)において、温度制御のためにNose-Hoover法がよく使われる。しかし、Nose-Hoover法を調和振動子に作用させるとエルゴード性が破れ、指定温度のカノニカル分布にいかないことが知られている。それを解決するためは、Kinetic-Moments法やNose-Hoover-Chain法などの多変数熱浴や、Langevin法などの確率的熱浴を使えば良い。
ここではなぜ、そしてどのようにNose-Hoover法ではエルゴード性が破れ、他の方法ではエルゴード性を回復するかを説明する。サンプルコードは
https://github.com/kaityo256/thermostats
においてある。
理論的背景
Nose-Hoover法
系として自然ハミルトン系
\[H = \frac{p^2}{2} + V(q)\]を考える1。ただし簡単のため質量は1としている。この系にNose-Hoover法をつけた時の運動方程式は
\[\begin{aligned} \dot{p} &= - \frac{\partial H}{\partial q} - \frac{\zeta p}{Q}\\ \dot{q} &= \frac{\partial H}{\partial p}\\ \dot{\zeta} &= p^2 - \frac{1}{\beta} \end{aligned}\]となる。ただし、$Q$は熱浴の質量、$\beta = 1/k_B T$は指定温度の逆温度である。この系の分布関数$f(p,q,\zeta)$の時間発展は、以下の連続の式で与えられる。
\[\frac{\partial f}{\partial t} = - \frac{\partial}{\partial p}(\dot{p} f) - \frac{\partial}{\partial q}(\dot{q} f) - \frac{\partial}{\partial \zeta}(\dot{\zeta} f)\]ここで、定常分布$f_\mathrm{eq}$は時間変化しないので、時間偏微分が0となって以下の式を満たす。
\[\frac{\partial}{\partial p}(\dot{p} f_\mathrm{eq}) + \frac{\partial}{\partial q}(\dot{q} f_\mathrm{eq}) + \frac{\partial}{\partial \zeta}(\dot{\zeta} f_\mathrm{eq}) = 0\]これに運動方程式を代入すると、定常分布は以下の形であることがわかる。
\[f_\mathrm{eq} \propto \exp\left[ -\beta (H + \frac{\zeta^2}{2Q}) \right]\]追加自由度$\zeta$はガウス分布になっているから積分により消去2できて指定温度のカノニカル分布が実現する。すなわち、Nose-Hoover法とは自由度を追加することで、追加自由度も含めたカノニカル分布を実現する手法である。
しかし、ハミルトニアンとして調和振動子$H=p^2/2 + q^2/2$を与えると、指定温度のカノニカル分布にならないことが知られている。カノニカル分布が実現しているかどうかは、エネルギーの累積分布関数を見るのが良い3。分布関数$f_\mathrm{eq}$が$\exp(-\beta E)$に比例しているので、その累積分布関数$P(E)$は
\[P(E) = 1 - \exp(-\beta E)\]で与えられる。したがって$P(E)$を$\exp(-\beta E)$に対してプロットすれば、$(1,0)$と$(0,1)$を結ぶ直線になるはずである。逆に、そうなっていなければカノニカル分布が実現していないことがわかる。
実際に、$Q=1$、$\beta = 1$として、Nose-Hoover法を調和振動子に適用させ、累積分布関数$P(E)$を計算した結果が以下のグラフである。
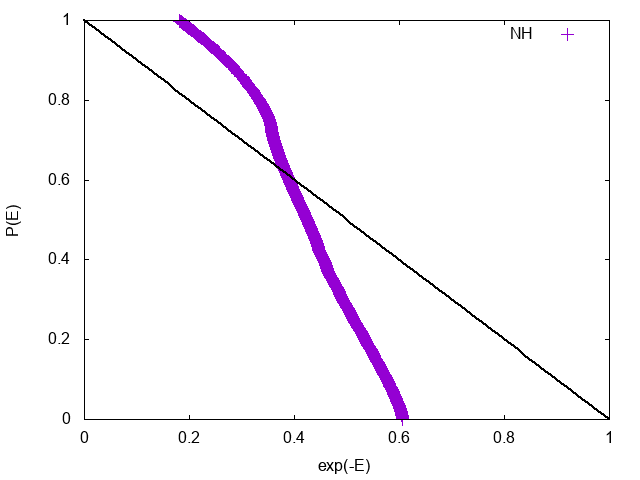
指定温度1のカノニカル分布になっていれば黒い直線に乗らなければならないが、明らかにずれている。
位相空間$(p,q)$はこうなっている。
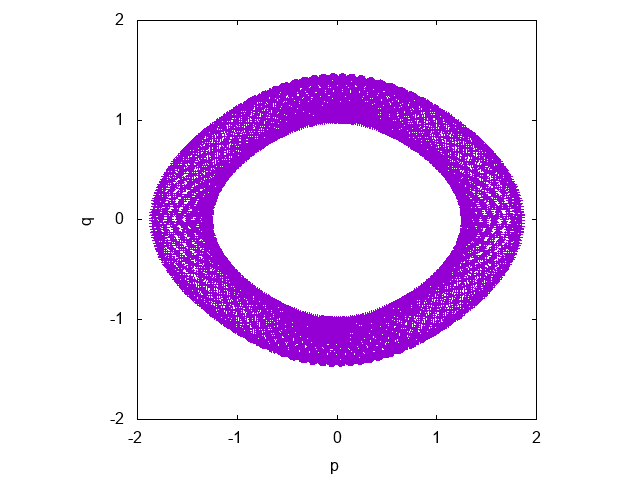
本来、原点に近いほど密に、遠いほど疎に、$\exp(-\beta E)$に比例して位相空間を軌道が埋め尽くさなければならないが、明らかにエネルギーに上限と下限が存在している。これがエルゴード性の破れである。
エルゴード性が破れる理由
調和振動子+Nose-Hoover法でエルゴード性が破れるのは、系に漸近的に非自明な保存量が構築されるからである。調和振動子にNose-Hooverをつけた系の運動方程式は以下の形になっている。
\[\begin{aligned} \dot{p} &= -q - \frac{p\zeta}{Q} \\ \dot{q} &= p \\ \dot{\zeta} &= p^2-1 \end{aligned}\]簡単のため、質量を1、指定温度も1としている。調和振動子は$(p,q)$平面をぐるぐるまわるので、極座標に取り直すのが自然であろう。そこで、変数変換$p = r \cos \theta, q = r \sin \theta$を施す。すると、運動方程式は
\(\begin{aligned} \dot{r} &= - \frac{r \zeta \cos^2 \theta}{Q} \\ \dot{\zeta} &= r^2 \cos^2 \theta -1 \end{aligned}\) ここで$Q$が十分に大きければ、$r$や$\zeta$に比べて$\theta$の運動は十分に早く、$\cos^2 \theta$はほぼ定数とみなして良いだろう(断熱近似)。そこで$\cos^2 \theta$を、その平均値$1/2$で置き換えると、
\[\begin{aligned} \dot{r} &= - \frac{r\zeta}{2Q} \\ \dot{\zeta} &= \frac{r^2}{2} -1 \end{aligned}\]これは変数分離型なので、以下の時間不変量(第一積分)を得る。
\[C = \frac{r^2}{2} + \frac{\zeta^2}{2Q} - \ln r^2\]ただし$C$は初期条件から決まる定数である。さて、$\zeta^2/2Q \geq 0$であり、$E=p^2/2 + q^2/2 = r^2/2$であるから、全エネルギー$E$は以下の不等式を満たす。
\[E - \frac{1}{2} \ln E \leq C + \ln2\]を得る。上記の左辺は下に凸な関数であるから、これはエネルギーに上限と下限があることに対応する。これがNose-Hoover法が調和振動子系においてエルゴード性を失う理由である(一般的な証明は参考文献を参照のこと)。
さて、Nose-Hoover法が調和振動子系でエルゴード性を失うのは、追加自由度が漸近的に変数分離型となり、非自明な保存量を構築してしまうからであった。したがって、熱浴自由度を増やしてしまえば求積できず、エルゴード性を回復することができる。そのような方針で作られたのがKinetic-Moments法やNose-Hoover-Chain法である。
Kinetic-Moments法
Kinetic-Moments法の運動方程式は以下のように与えられる。
\[\begin{aligned} \dot{p} &= - \frac{\partial H}{\partial q} - \frac{\zeta p}{Q_\zeta} - \frac{\eta p^3}{Q_\eta}\\ \dot{q} &= \frac{\partial H}{\partial p}\\ \dot{\zeta} &= p^2 - \frac{1}{\beta} \\ \dot{\eta} &= p^4 - \frac{3 p^2}{\beta} \end{aligned}\]これはNose-Hoover法が$p^2$を制御するのに加え、$p^4$も制御しようという手法である。熱浴の質量$Q_\zeta$と$Q_\eta$はそれぞれ追加自由度$\zeta$と$\eta$の質量に対応する。
\[f_\mathrm{eq} \propto \exp\left[ -\beta (H + \frac{\zeta^2}{2Q_\zeta}+\frac{\eta^2}{2Q_\eta}) \right]\]を満たすことを示すのは容易であろう。
Nose-Hoover-Chain法
また、$p$を二変数で制御するのではなく、追加自由度$\zeta$を制御することもできる。それが以下の運動方程式で与えられるNose-Hoover-Chain法である。
\[\begin{aligned} \dot{p} &= - \frac{\partial H}{\partial q} - \frac{\zeta p}{Q_\zeta}\\ \dot{q} &= \frac{\partial H}{\partial p}\\ \dot{\zeta} &= p^2 - \frac{1}{\beta} - \frac{\eta \zeta}{Q_\eta} \\ \dot{\eta} &= \frac{\zeta^2}{Q_\zeta} - \frac{1}{\beta} \end{aligned}\]これもKinetic-Moments法と同じ定常分布を持つ。
Langevin法
決定論的熱浴ではなく、確率的な方法を用いることもできる。以下のような運動方程式を考える。
\[\begin{aligned} \dot{p} &= - \frac{\partial H}{\partial q} - \gamma p + R\\ \dot{q} &= \frac{\partial H}{\partial p}\\ \end{aligned}\]ここで$\gamma$は定数、$R$は$\left< R(0)R(t) \right> = 2D\delta(t)$を満たす揺動力である。分布関数の時間発展は
$$ \frac{\partial f}{\partial t} =
- \frac{\partial}{\partial p}\left( -\frac{\partial H}{\partial q} - \gamma p -D \frac{\partial}{\partial p} \right)f
- \frac{\partial}{\partial q} \left( \frac{\partial H}{\partial p} \right)f $$ となる。ここで揺動力$R$が微分に化けることに注意4。上記の定常分布が、$\beta = \gamma/D$を満たす逆温度についてのカノニカル分布が定常分布となることを確認することは容易であろう。
前置きが長くなったが、Kinetic-Moments, Nose-Hoover-Chain, Langevin、以上3つの手法について、調和振動子系がたしかにカノニカル分布になることを確認しましょう、というのが本稿の趣旨である。
数値計算
Nose-Hoover法(NH)、Kinetic-Moments法(KM)、Nose-Hoover-Chain法(NHC)については4次のRunge-Kutta法を用いる5。Langevin法のような確率的な微分方程式は、Runge-Kuttaをそのまま適用するとおかしなことになる。おそらくそういうのをちゃんと数値積分する手法はあるのだろうが、どうせ揺動力を含むから精度がいらないので、1次のEuler法で解いてしまおう。温度は1、熱浴質量1、調和振動子の質量を1として、時間刻み0.001で10000000ステップほど計算させよう。
まずはエネルギーの累積確率分布はこうなる。
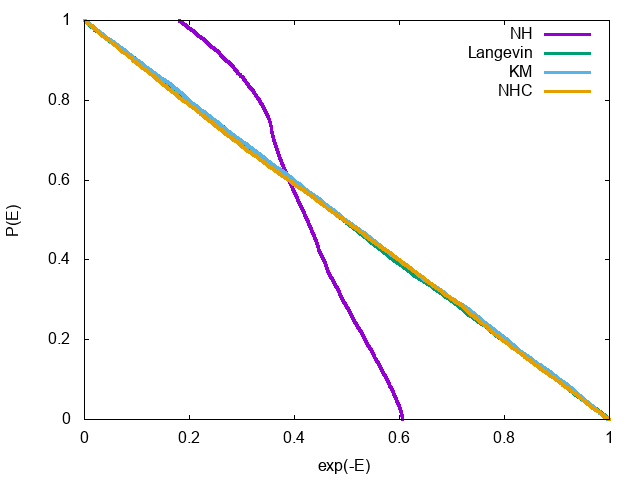
Nose-Hoover系以外は理論曲線に載っている、すなわち指定温度のカノニカル分布を実現していることがわかる。
位相空間はこんな感じ。
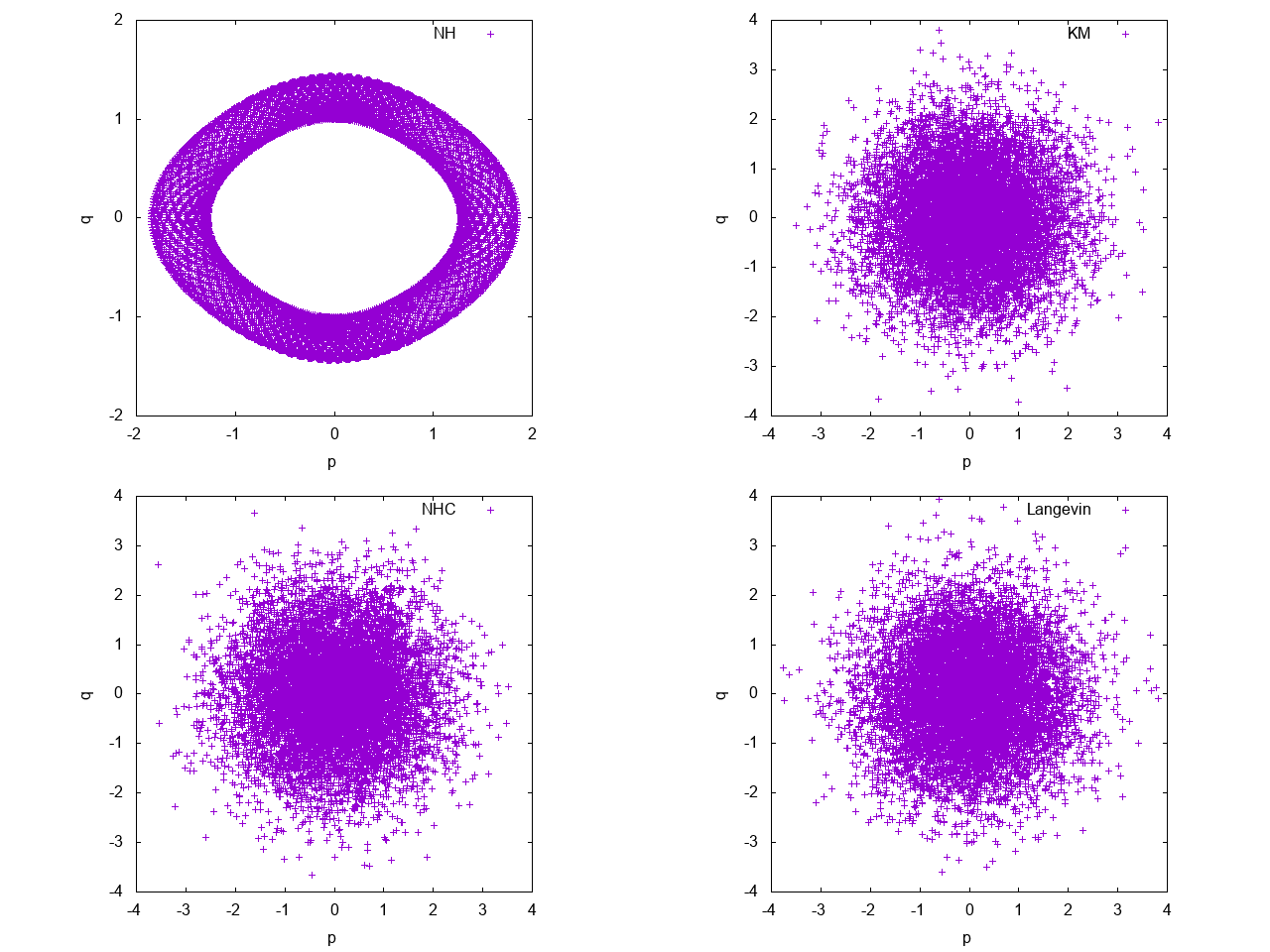
Nose-Hoover以外はちゃんと温度が制御できていそうなのがわかる。
まとめ
調和振動子にNose-Hoover熱浴をつけた場合にエルゴード性が破れること、また多変数熱浴や確率的熱浴をつけるとエルゴード性を回復することを示した。たまに「少数自由度系に熱浴をつけるとエルゴード性を失う」と誤解されているが、調和振動子系がエルゴード性を失うのは、系の自由度とカップルした熱浴自由度が漸近的に保存量を構築するからで、系が少数自由度であることとは本質的に無関係である。したがって、系が大自由度系であっても、調和振動子的な振る舞いを見せる部分系があれば、エルゴード性は破れ得る。また、「熱浴変数が多変数であればあるほど安定」という誤解もあるが、適切な熱浴変数が2変数以上あれば運動方程式は求積できず、したがってエルゴード性も破れないため、それ以上の自由度は、緩和時間はともかく少なくともエルゴード性には無関係である6。
参考文献
- Nose-Hoover 法: W. G. Hoover, Phys. Rev. A vol. 31, 1695 (1985).
- Langevin 法: M. P. Allen and D. J. Tildesley, Computer Simula- tion of Liquids (Oxford University Press, 1989), ISBN 0198556454.
- Kinetic-Moments 法: W. G. Hoover and B. L. Holian, Phys. Lett. A vol. 211, 253 (1996).
- Nose-Hoover-Chain 法: G. J. Martyna, M. L. Klein, and M. Tuckerman, The Journal of Chemical Physics vol. 97, 2635 (1992).
- 調和振動子でエルゴード性が破れる証明: H. Watanabe and H. Kobayashi, Phys. Rev. E vol. 75, 040102 (2007).
-
Nose-Hoover法については分子動力学法ステップ・バイ・ステップ その5も参照。 ↩
-
$\zeta$に関して積分することで自由度を消去できる。これは$(p,q,\zeta)空間から$$(p,q)$平面に射影したことに対応する。 ↩
-
累積分布関数の求め方については累積分布関数をソートで求めるも参照。 ↩
-
詳細についてはFokker–Planck方程式やKramers-Moyal展開について調べてください。 ↩
-
微分方程式と数値積分法を自由に組み合わせる方法についてはRunge–Kutta法を関数オブジェクトでを参照。 ↩
-
ただし、ここでいうエルゴード性とは「系に非自明な保存量が構築されることで軌道が制限される」ことを指している。文脈によっては別の定義のエルゴード性を用いている場合もあるので注意。 ↩
 A Robot’s Sigh
A Robot’s Sigh