頂点被覆問題のグラフによる可視化

はじめに

頂点被覆問題(Vertex Cover Problem)は、典型的なNP完全の問題であるので、アルゴリズムの題材として取り上げたい。で、これはグラフ理論の問題なので、グラフを用いて考えるとわかりやすい。一方、現実に現れる問題としては、テーブル表記の方がわかりやすい。

さて、頂点被覆問題のソルバを作ったは良いが、それをセミナーとかで説明する際に適切なサンプルを作るのが結構面倒だったので、説明用のデータを作るRubyスクリプトを作った。

https://github.com/kaityo256/mhs_graph

これを使うと、自動的に頂点被覆問題、その解答、そのグラフ可視化のセットを出力してくれるので、講義とかプログラム演習の課題とかに使うのに便利だと思われる。

使い方

スクリプトの実行にはrubygemとgraphvizが必要なので、適宜インストールしておく。スクリプトを実行すると、標準出力に以下のようなものを吐く。

$ ruby mhs_graph.rb 5 2 

Input Condition
|   | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 1 | - | O | - | O | - | O | O |
| 2 | O | - | O | O | - | - | - |
| 3 | O | O | - | - | O | - | - |
| 4 | - | - | O | - | O | O | - |
| 5 | - | - | - | - | - | - | O |

Minimal Hitting Sets
4,2,1
3,2,1
5,4,3,2
4,3,1

Saved as input.dat
Saved as input.bit
Saved as mhs.dat
Saved as mhs.bit
Saved as graph.png
Saved as graph_mhs0.png
Saved as graph_mhs1.png
Saved as graph_mhs2.png
Saved as graph_mhs3.png

これは、入力条件のテーブル表現、その解答である極小ヒッティングセット(Minimal Hitting Set)の列挙、その他保存したファイル名の一覧である。

インプットパラメタは以下の通り。

$ ruby mhs_ruby.rb size seed
  • size: 問題のサイズ。デフォルトは5。かなり富豪的なプログラムになっているので、あまり大きくしないほうが良い。せいぜい10まで。
  • seed: 乱数のシード。デフォルトは-1。-1を指定するとシードを設定しない。

seedを指定しないと、実行するたびに異なる結果が得られるので、好みのグラフが出力されるまで何度も実行すれば良いと思われるが、「あっ、さっきの奴の方が良かったのに」と思っても再現できなくなるので、適当にシード変えながら与えて実行すると良いかも。

以下、上記の例について何が出力されているか解説する。

解説

例えばあなたがある地域のピザのデリバリーサービスを開業したいとする。その地域はいくつかのエリアにわかれており、配達ではその全てをカバーしたい。従業員の候補者は、配達可能なエリアが決まっており、なるべく少ない従業員数で開業するには誰と誰を雇えば良いだろうか？これが最小頂点被覆問題(Minimum Hitting Set Problem)である。

例えば地域がA-Gの7つのエリアにわかれており、候補者が5人いるとする。それぞれの候補者の配達可能エリアが以下のように与えられたとする。

  A B C D E F G
1 - O - O - O O
2 O - O O - - -
3 O O - - O - -
4 - - O - O O -
5 - - - - - - O

1番目の候補者はB,D,F,Gの4エリアについて配達可能だが、5番目の候補者はエリアGのみ配達可能、といった具合。

上記について、スクリプトは以下の候補を出力する。

Minimal Hitting Sets
4,2,1
3,2,1
5,4,3,2
4,3,1

これは、例えば「1,2,4」の3名を雇えば全エリアをカバーできますよ、というもの。ここで列挙しているのは極小頂点被覆(Minimal Hitting Set, MHS)である。どの要素を除いても頂点被覆でなくなる、というのが極小頂点被覆の定義であり、最小頂点被覆は、極小頂点被覆のうち最も要素数が少ないもののことである。

グラフ表現

さて、サンプルの表をよく見ると、各エリアを担当可能な人は二人ずついる。テーブルを転置するとわかりやすい。

  1 2 3 4 5
A - O O - -
B O - O - -
C - O - O -
D O O - - -
E - - O O -
F O - - O -
G O - - - O

それぞれのエリアを配達可能な候補者が二人ずついるのがわかるだろう(そうなるようにスクリプトがサンプルを作ってくれる)。ここで、候補者を頂点(Vertex)とし、エリアを候補者をつなぐ辺(Edge)としてグラフ表現ができる。そうして作ったグラフは以下のようなgraph.pngとして保存される。

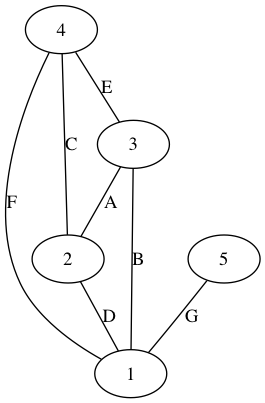
image0.png

頂点に候補者を、辺にエリア名を記載してある。例えばエリアGに配達可能な人は1番と5番の候補者であることを表現している。我々は全エリアをカバーしたいのであるから、全ての辺が選ばれた頂点に接しているという条件で、なるべく少ない頂点を選びなさい、という問題になる。これが頂点被覆問題(Vertex Cover Problem)と呼ばれる所以である。この問題は、辺(Edge)が2つ以上の頂点を結ぶ場合に拡張され、そのようなグラフをハイバーグラフ、ハイパーグラフ上での頂点被覆はヒッティングセット(Hitting Set)と呼ばれることが多いので、ここでもヒッティングセット問題と呼ぶことにする。

スクリプトが出力した候補はこんな感じだった。

Minimal Hitting Sets
4,2,1
3,2,1
5,4,3,2
4,3,1

これは、例えば「4,2,1」を選びなさい、ということなので、それを赤く塗ったものがgraph_mhs0.png,graph_mhs1.png,…として出力される。

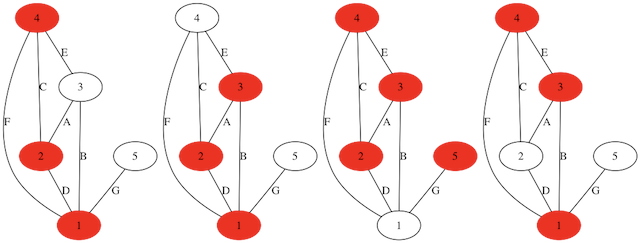
image1.png

上記の4例において、全ての辺が赤く塗られた頂点に接しているのがわかるだろう。このように選ばれた頂点のセットを頂点被覆(Hitting Set)と呼ぶ。また、上記の例において、どの赤い頂点を抜いても、カバーされない辺が出現する。この条件を満たす頂点被覆を極小頂点被覆(Minimal Hitting Set)1と呼ぶ。その中で最も要素数が少ないものが最小頂点被覆(Minimum Hitting Set)である。

ビット表現

先の転置した表を再掲する。

  1 2 3 4 5
A - O O - -
B O - O - -
C - O - O -
D O O - - -
E - - O O -
F O - - O -
G O - - - O

ここで、それぞれの行をビット列で表現することを考えよう。上記の表は以下のビット列で表現できる。

00110
00101
01010
00011
01100
01001
10001

スクリプトを実行すると、上記をinput.bitという名前で保存する。 通常、ビットの上位ビットを左に書くため、1番目のビットを右に、5番目のビットを左に、つまり左右反転した形で表現していることに注意。さて、A-G全てをカバーするとは、この7つのビット列全てとAND(論理積)をとってゼロでないビット列を探しなさい、ということと等価である。

極小頂点被覆をビット表現したものはmhs.bitという名前で保存される。

01011
00111
11110
01101

このうち、例えば最初の列01011が、7つ全てのビット列とANDを取ってゼロでないことは容易に確認できるであろう。

また、これらを配列の形で表現したものも出力されるので、適宜参考にされたい。

3,2
3,1
4,2
2,1
4,3
4,1
5,1

4,2,1
3,2,1
5,4,3,2
4,3,1

まとめ

頂点被覆問題を自動で作って、解いて、それをグラフ化してくれるスクリプトを作った。ついでにテーブルをMarkdown形式で吐いてくれるので地味に便利だと思われる。頂点被覆問題(集合被覆問題)は最適化問題、グラフ理論、ビット演算といろんな見方ができるので、NP完全とかNP困難とかの問題の題材に適していると思われる。講義やセミナーにこのスクリプトを活用していただければ幸いである。

その他

その他の話題いろいろ。

ハイパーグラフ

上記の例ではグラフ化するために、各辺が必ず２つの頂点を結んでいた。これは、各エリアに配達可能な候補者が二人ずついることに対応するが、現実の問題では、あるエリアを配達可能な候補者が1人だったり、3人以上いたりするだろう。これは辺(Edge)が1つや3つ以上の頂点(Vertex)を結んでいることに対応し、ハイパーエッジ(Hyper Edge)と呼ばれる。ハイパーエッジを含むグラフをハイパーグラフ(HyperGraph)と呼ぶ。ハイパーグラフの可視化は難しい(面倒くさい)のでやらなかった。興味のある方は挑戦されたい。

重み付き集合被覆

頂点被覆問題と集合被覆問題は等価である。また、集合被覆問題は一般に重み付きのものが問題設定がされることが多い。上記の例なら、5人の候補者に賃金が設定されており、7つのエリアをカバーしつつ、賃金の合計を最小化したい、といった問題になる。例えば多くのエリアをカバーできる人は、それだけ賃金が高い、といった問題設定となるだろう。それをどうやって解くか、厳密に解くか、それとも近似アルゴリズムで解くか、といった問題が発展問題として考えられる。が、重み付きの問題を自動で作るのは面倒だったのでやらなかった。興味のある人は挑戦されたい。

グラフの連結

適当に問題を作ると、グラフ化した際に問題が分裂することがある。例えば以下のような問題設定を考える。

  A B C D E
1 - - - O -
2 - - - - O
3 - - O O -
4 - O - - O
5 - O - - -
6 O - O - -
7 O - - - -

7人の候補者が5つのエリアをカバーしようとしている。これをグラフ化すると以下のようになる。

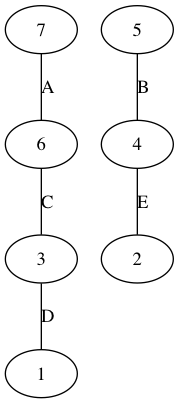
image2.png

1,3,6,7のグループと、2,4,5のグループに分裂してしまった。これでは問題として不適切なので、適当に作ったグラフが連結であるかをチェックし、連結でなければ再度作りなおすようにしている。そして10000回作り直してダメだったらあきらめている。最初から連結になるように作るエレガントな方法があるかもしれない。興味のある方は(r

エリアの数の決め方

入力として与えられるのは候補者の数のみで、エリアの数は勝手に決まる。これは

  • 候補者をランダムに二人選んで、その二人が配達可能なエリアとして追加する
  • 候補者が全員選ばれるまで上記を繰り返す

という形でエリアの数を決めているからである。さらに、候補者を普通にランダムに選ぶと、全く同じ組み合わせが出てきてしまう。そこで、

  • 最初に候補者から二人選ぶやり方を全て列挙する
  • その配列をシャッフルする
  • 上から順番に追加していって、候補者が全員選ばれたらおしまい

という形をとっている。当該ソースはこんな感じ。

def make_input_sub(n)
  t = 0
  tmax = (1 << $max) -1
  a = Array.new($max){|i| i+1}
  b = a.combination(2).to_a.shuffle
  r = []
  b.each do |x,y|
    te = (1 << (x-1)) | (1 << (y-1))
    r.push te
    t = t | te
    break if t == tmax
  end
  r
end

上の方で富豪的と書いたのはそういう事情による2。これだと大きなサンプルデータを作れないので、興味のある方は(r

  1. 頂点被覆はVertex Coverであるが、ハイパーグラフに拡張した場合の頂点被覆はヒッティングセット(Hitting Set)と呼ぶことが多いので、ここでもその呼称を用いる。 ↩

  2. いや、もっと良い方法あるんだろうけど、どうせグラフで可視化する頂点って10とかのオーダーなんで、それなら組み合わせ全列挙してシャッフルしちゃったほうが楽だなぁ、と思って(手抜き)。 ↩